递归定义
递归是一种非常重要的算法思想,递归,在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。简单来说,递归表现为函数调用函数本身。有一个例子很形象:
递归最恰当的比喻,就是查词典。我们使用的词典,本身就是递归,为了解释一个词,需要使用更多的词。当你查一个词,发现这个词的解释中某个词仍然不懂,于是你开始查这第二个词,可惜,第二个词里仍然有不懂的词,于是查第三个词,这样查下去,直到有一个词的解释是你完全能看懂的,那么递归走到了尽头,然后你开始后退,逐个明白之前查过的每一个词,最终,你明白了最开始那个词的意思。
递归特点
实际上,递归有两个显著的特征,终止条件和自身调用:
- 自身调用:原问题可以分解为子问题,子问题和原问题的求解方法是一致的,即都是调用自身的同一个函数。
- 终止条件:递归必须有一个终止的条件,即不能无限循环地调用本身。
深入理解递归过程
用以下代码来说明递归的执行过程,若输入字符为 abc\n,则执行函数输入为什么呢?
#include<iostream>
using namespace std;
int recur()
{
char c;
c = cin.get();
if (c != '\n')
recur();
cout << c;
return 0;
}
int main()
{
recur();
return 0;
}
递归的执行成功如下图所示:
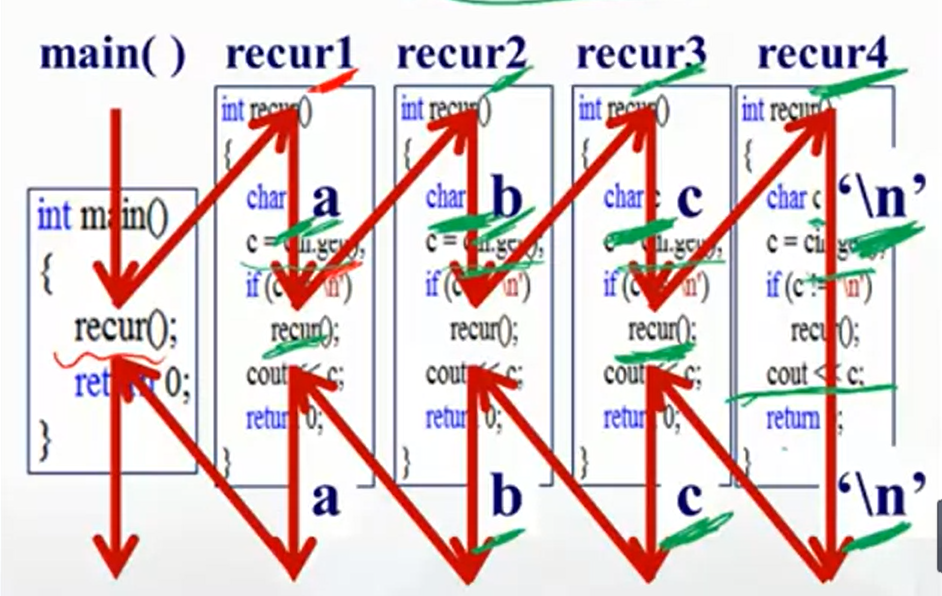
需要注意的地方是,当递归被调用之后仍会向下执行,即执行 recu3 时,会执行 ` cout « c;` ,所以执行结果为
abcd
dcba
再看一下例子
oid funC()
{
puts("funC");
}
void funB()
{
funC();
puts("funB");
}
void funA()
{
funB();
puts("funA");
}
假如调用函数 funA ,那么它就会调用函数 funB,funB 再调用 funC,funC 打印出”funC”,此时 funC 执行完毕返回至 funB 继续执行,打印出”funB”,然后 funB 执行完毕返回至 funA,funA打印”funA”,执行完毕,执行结果如下所示
funC
funB
funA
可以看出来,每次调用一次函数,都是等它彻底执行完毕之后,才会返回去继续执行,那么如果将每个函数“展开”,大概就像这样
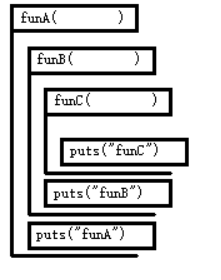
每一个大框代表一次函数调用,这样可以很直观的看出程序执行过程(按图从上至下即可)。“每调用一次函数,都是等它彻底执行完毕之后,才会返回去继续执行”这句话的含义,体现在图中就是一个框被整个包裹在另一个框之中。
其实递归也是如此,从根本上来说,递归调用其实调用的并不是本身,你写在程序里的一个函数,调用它其实并不是真的执行了它,而是开辟了一份空间,把其中的数据(包括参数,和函数里的一些变量等),存在其中,然后根据你写的代码去修改这些数据,每次调用一个函数,就会开辟一份这样的空间,执行完毕之后释放,而递归的时候,每一次递归调用都会开辟一份这样的空间,互相独立,所以才有本段开头的一句话,所以,如果一次递归调用共调用了N次,你就可以理解为你写了N个函数,只不过它们长得一样罢了。
举个例子,经典的递归求阶乘,如果我们想要算出n!,只需要先算出(n-1)!再乘n就可以了(递归求阶乘其实是相当差的一个方法,这里仅做举例):
int fact(int n)
{
if(n==0)return 1;
else return fact(n-1)*n;
}
fact(4)的执行过程如下:
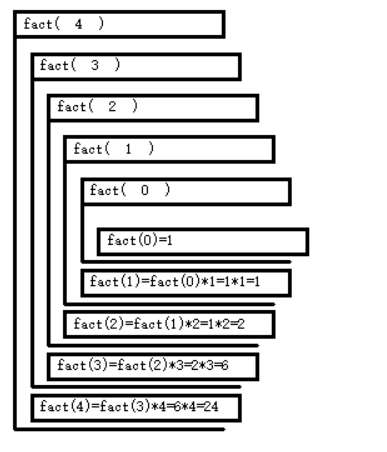
当计算fact(1)时,就是先算出了fact(0)=1,然后才能知道fact(1)是1*1=1。
当计算fact(2)是,也是先算出了fact(1)=1,然后才能知道fact(2)是1*2=2。
其他也类似。
从图中还可以看出来,每一次递归调用,都是彻底执行完这一次调用,才会返回(经过一个函数框的下边框就意味着返回了)。
递归解题思路
解决递归问题一般就三步曲,分别是:
- 第一步,定义函数功能
- 第二步,寻找递归终止条件
- 第三步,递推函数的等价关系式
递归应用
用阶乘递归举例
- 定义函数功能 定义函数功能,就是说,你这个函数是干嘛的,做什么事情,换句话说,你要知道递归原问题是什么呀?比如你需要解决阶乘问题,定义的函数功能就是n的阶乘,如下:
//n的阶乘(n为大于0的自然数)
int factorial (int n){
}
- 寻找递归终止条件 递归的一个典型特征就是必须有一个终止的条件,即不能无限循环地调用本身。所以,用递归思路去解决问题的时候,就需要寻找递归终止条件是什么。比如阶乘问题,当n=1的时候,不用再往下递归了,可以跳出循环啦,n=1就可以作为递归的终止条件,如下:
//n的阶乘(n为大于0的自然数)
int factorial (int n){
if(n==1){
return 1;
}
}
- 递推函数的等价关系式 递归的「本义」,就是原问题可以拆为同类且更容易解决的子问题,即「原问题和子问题都可以用同一个函数关系表示。递推函数的等价关系式,这个步骤就等价于寻找原问题与子问题的关系,如何用一个公式把这个函数表达清楚」。阶乘的公式就可以表示为 f(n) = n * f(n-1), 因此,阶乘的递归程序代码就可以写成这样,如下:
int factorial (int n){
if(n==1){
return 1;
}
return n * factorial(n-1);
}
递归存在的问题
- 递归调用层级太多,导致栈溢出问题
- 递归重复计算,导致效率低下
