总结及例题

1.1　算法的规范化和量化度量

冯·诺依曼发明计算机体系结构和高德纳编写TeX程序似乎都是偶然为之的结果。冯·诺依曼原本不想发明计算机，他只想算题；高德纳也不想发明排版软件，他只想写书。为什么这些大师们偶然为之的工作比二流人才穷其一生的发现有时还有影响力呢？因为除了能力的差异外，他们还有着遇到问题时解决问题的积极态度。任何人在前进的过程中都会遇到问题，但是对待问题的态度决定了个人的命运。

1.2 大数和数量级的概念

场景1：使用1万个数据进行测试，算法A运行1毫秒，算法B则需要运行10毫秒。

场景2：使用100万个数据进行测试，算法A运行10000毫秒，算法B运行6000毫秒。

那么到底哪个算法更好一些呢？如果单纯从场景1做判断，显然是算法A好，而单看场景2，似乎算法B更优。按照普通人的思维，他可能会说，数据少的时候算法A好，数据多的时候算法B好，然后还津津乐道自己懂得辩证法，懂得具体问题具体分析。但计算机科学比较认死理，不搞变通，不玩辩证法，它要求我们制定一个明确的、一致的标准，不要一会儿这样，一会儿那样。那么问题就来了，我们应该怎样制定这个标准呢？

高德纳的思想主要包括以下几个部分。

1．在比较算法的快慢时，只需要考虑数据量特别大，大到近乎无穷大时的情况。为什么要比大数的情况，而不比小数的情况呢？因为计算机的发明就是为了处理大量数据的，而且数据越处理越多。比如我和同学们做砸的那个对账功能，就是没有考虑数据量会剧增。

2．决定算法快慢的因素虽然可能有很多，但是所有的因素都可以被分为两类：第一类是不随数据量变化的因素，第二类是随数据量变化的因素。

比如说有两种算法：第一种的运算次数是\(3N^2\)，其中N是处理的数据量；第二种则是100NlogN。前面的那个3也好，这里的100也罢，都是常数，和N的大小显然没有关系，处理10个、100个、1亿个数，都是如此。但是后面和N有关的部分则不同，当N很大时，N2要比NlogN大得多。在处理几千，甚至几万个数字的时候，这两种算法差异不明显，但是高德纳认为，我们衡量算法好坏时，只需要考虑N近乎无穷大的情况。为什么这么考虑问题呢？因为计算机的任务是处理远远超出我们想象的规模的数据量，而我们的认知其实很难想象那样规模的数据有多少。

例题1.1

围棋有多复杂？

答：棋盘上每一个点最终可以是黑子、白子或者空位三种情况，而棋盘有361个交叉点，因此围棋的变化最多可以有3361≈2×\(10^{172}\)种情况。这个数当然相当大，大约是2后面跟172个零。

例题1.2

一句有20个单词的英语语句可以有多少种组合？

答：英语的单词数在10万个以上，这里就算是10万个（即\(10^5\)），20个单词不受限制的组合数是\(((10)^5)^{20}=10^{100}\)。

例题1.3

给定一个实数序列，设计一个最有效的算法，找到一个总和最大的区间。

解法1： 做一次三重循环，即中学里学的排序组合的方法。

定义两个指针，分别模拟区间的两端，对应代码中的前两个for循环；
定义一个循环，遍历两个指针的数据，计算区间总和；
比较每次总和的结果，遇到最大值则保留值和区间两端的索引。

#include <iostream>
#include <vector>
#include <cfloat>

using namespace std;


class Solution{
public:
    pair<int, int> maxSum(double *nums, int size) {
        pair<int, int> result;

        double maxValue = -DBL_MAX;
        int p = 0,q = 0;
        for(int i = 0; i < size; i++) {
            for(int j = i ; j < size; j++) {
                double temp = 0.0;
                for(int k = i; k <= j; k++) {
                    temp += nums[k];
                }
                if(temp > maxValue) {
                    maxValue = temp;
                    p = i;
                    q = j;
                }

            }
        }
        result = make_pair(p, q);
        return result;
    }
};

int main() {
    Solution solution;
    int _size = 12;
    double _nums[] = {1.5, -12.3,3.2,-5.5,23.2,-1.4,-12.2,34.2,5.4,-7.8,1.1,-4.9};
    auto res = solution.maxSum(_nums,_size);
    cout << res.first <<" " <<res.second <<endl;
}


  

算法时间复杂度：\(O(N^3)\)

解法2： 做两重循环。解法1利用一次循环单独计算了两端之和，这里将此步骤进行简化。

定义两个指针，分别模拟区间的两端，对应代码中的前两个for循环；
在每次循环时，记录总和值，并与总和最大值进行比较；
剪枝操作，若元素值<=0时，则不用比较，肯定小于最大值，但为了保证区间连续性，仍需要添加元素值。

#include <iostream>
#include <vector>
#include <cfloat>

using namespace std;


class Solution{
public:
    pair<int, int> maxSum(double *nums, int size) {
        pair<int, int> result;

        double maxValue = -DBL_MAX;
        int p = 0,q = 0;
        for(int i = 0; i < size; i++) {
            double sum = 0.0;
            for(int j = i ; j < size; j++) {
                sum += nums[j]; //先添加元素值，保证区间连续性
                if(nums[j] <= 0.0) continue; // 值<0,不用比较大小，结束本次循环
                if(sum > maxValue) {
                    maxValue = sum;
                    p = i;
                    q = j;
                }
            }
        }
        result = make_pair(p, q);
        return result;
    }
};

int main() {
    Solution solution;
    int _size = 12;
    double _nums[] = {1.5, -12.3,3.2,-5.5,23.2,-1.4,-12.2,34.2,5.4,-7.8,1.1,-4.9};
    auto res = solution.maxSum(_nums,_size);
    cout << res.first <<" " <<res.second <<endl;
}

  

算法时间复杂度：\(O(N^2)\)

解法3： 利用分治算法。

将序列[p,q]一分为二，分成从p到K/2，以及K/2+1到q两个子序列[p, K/2]和[K/2+1,q]；
对这两个子序列分别求总和最大区间；
- 情况1：两个子序列的总和最大区间连续。
  - 若两个区间各自的和均为正整数，总和最大区间为[p,q];
  - 否则，选取两个子序列的总和最大区间中大的一个；
- 情况2：两个子序列的总和最大区间不连续。假设分别为[p1,q1]、[p2,q2]。
  - 选择[p1,q1]、[p2,q2]和[p1,q2]中的最大的一个。
归并步骤。

#include <iostream>
#include <vector>
#include <cfloat>

using namespace std;


class Solution{
public:
    pair<int, int> maxSum(double *nums, int size) {

        auto result = findMaxSumRange(nums, 0, size - 1);
        return make_pair((int)result[0], (int)result[1]);
    }
    vector<double> findMaxSumRange(double *nums, int start, int end) {
        if(start == end) {
            vector<double> result = {(double)start, (double)end, nums[start]};
            return result;
        }
        int middle = (start + end) / 2;

        auto result1= findMaxSumRange(nums, start, middle);
        auto result2= findMaxSumRange(nums, middle+1, end);
        if(result1[1] == result2[0] + 1) { // 1. 两个子区间相连
            if(result1[2] > 0 && result2[2] > 0) { // 1.1 均为正整数
                vector<double> result =  {result1[0], result2[1], result1[2] + result2[2]};
                return result;
            }
            return result1[2] > result2[2]? result1:result2; // 1.2 取最大的一个
        }else { //2. 两个子区间不相连，取最大的一个
            double count = 0.0;
            for(int i = (int)result1[0]; i <= (int)result2[1]; i++) {
                count += nums[i];
            }
            vector<double> result3 = {result1[0], result2[1], count};
            auto temp = result1[2] > result2[2]? result1:result2;
            return temp[2] > count? temp:result3;
        }
    }

};


int main() {
    Solution solution;
    int _size = 12;
    double _nums[] = {1.5, -12.3,3.2,-5.5,23.2,-1.4,-12.2,34.2,5.4,-7.8,1.1,-4.9};
    auto res = solution.maxSum(_nums,_size);
    cout << res.first <<" " <<res.second <<endl;

}

  

算法时间复杂度：\(O(NlogN)\)

解法4： 正反两遍扫描。

扫描找到第一个大于零的数，若不存在，则最大的数则为要找的区间；
将左边界固定在第一个数，找到最大值及最大值的右边界；
- 若发现S(p, q)值小于0,则需要从q开始，反向计算区间和，找到值最大的索引（即最大区间和的左边界）；
  - 调转到q+1开始往后扫描，确定条件为while(q + 1 < size && nums[q] <= 0) q++;
  - 重复判断S(p, q)上述过程，计算每次区间的和，并与最大值maxValue进行对比；
  - 若大于最大值maxValue，则保存
- 若大于0，则判断区间和的大小；

#include <iostream>
#include <vector>
#include <cfloat>

using namespace std;


class Solution{
public:
    pair<int, int> maxSum(double *nums, int size) {
        pair<int, int> result;
        double maxValue = -DBL_MAX;
        int p = -1, q = 0;

        int maxLeft, maxRight;

        // 1. 数组中的值都小于等于0
        for(int m = 0; m < size; m++) {
            if (nums[m] > 0) {
                p = m;
                break;
            }
            if(maxValue < nums[m]) {
                maxLeft = m;
                maxRight = m;
                maxValue = nums[m];
            }
        }

        // 值都小于等于0
        if(p == -1) return make_pair(maxLeft, maxRight);

        // 2. 数组中存在大于0的数
        maxLeft = p; // 最大左边界
        int r = p; // 循环指针
        double lSum = 0.0;
        while(r < size) {
            lSum += nums[r];

            // 2.1 如果总和小于0，则反向计算
            if(lSum < 0) {
                int q = r;
                double rSum = 0.0;
                double maxRSum = -DBL_MAX;
                int tempL = 0;
                for(int i = q; i >= p; i--) {
                    rSum += nums[i];
                    if(rSum > maxRSum) {
                        maxRSum = rSum;
                        p = i;
                    }
                }

                double temp = 0.0;
                for(int j = p; j <= q; j++) {
                    temp += nums[j];
                }

                // 判断区间和与maxValue的大小
                if(maxValue < temp) {
                    maxValue = temp;
                    maxLeft = p;
                    maxRight = q;
                }
                // 查找下一段的起点
                while(q + 1 < size && nums[q] <= 0) {
                    q++;
                }
                p = q;
                r = q;
                lSum = 0;

            }else { // 2.2 如果总和大于等于0
                // 判断区间和与lSum的大小
                if(maxValue < lSum) {
                    maxValue = lSum;
                    maxLeft = p;
                    maxRight = r;
                }
                r++;
            }
        }

        result = make_pair(maxLeft,  maxRight);
        return result;
    }
};

int main() {
    Solution solution;
    int _size = 12;
    double _nums[] = {1.5, -12.3,3.2,-5.5,23.2,-1.4,-12.2,34.2,5.4,-7.8,1.1,-4.9};
    auto res = solution.maxSum(_nums,_size);
    cout << res.first <<" " <<res.second <<endl;
}

  

算法时间复杂度：\(O(N)\)

解法5： 使用动态规划求解。

用dp[i]表示以第i个元素为结尾的子数组的最大和,问题就转化为求max(dp);
dp[i]只有两个方向可以推出来：
- dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和;
- nums[i]，即：从头开始计算当前连续子序列和;
- 递推公式为：dp[i] = max(dp[i - 1] + nums[i], nums[i]);
dp数组初始化，dp[0]应为nums[0];
从左往右遍历；
- 若dp[i - 1] + nums[i] > nums[i],则改变右边界；
- 否则，重新计算，重置左右边界；
- 找到最大的子序和对应的左右边界。

#include <iostream>
#include <vector>
#include <cfloat>

using namespace std;


class Solution{
public:
    pair<int, int> maxSum(double *nums, int size) {

        int maxLeft = 0, maxRight = 0;
        int left, right;
        vector<double> dp(size);
        dp[0] = nums[0];
        double maxSum = nums[0];
        for(int i= 1; i < size; i++) {
            if(dp[i -1] + nums[i] > nums[i]) {
                dp[i] = dp[i - 1] + nums[i];
                maxRight = i;
            }else {
                dp[i] = nums[i];
                maxLeft = i;
                maxRight = i;
            }

            if(dp[i] > maxSum) {
                maxSum = dp[i];
                left = maxLeft;
                right = maxRight;
            }
        }
        return make_pair(left, right);
    }
};


int main() {
    Solution solution;
    int _size = 12;
    double _nums[] = {1.5, -12.3,3.2,-5.5,23.2,-1.4,-12.2,34.2,5.4,-7.8,1.1,-4.9};
    auto res = solution.maxSum(_nums,_size);
    cout << res.first <<" " <<res.second <<endl;
}
  

简化空间复杂度：将数组使用数值代替。代码如下：

#include <iostream>
#include <vector>
#include <cfloat>

using namespace std;


class Solution{
public:
    pair<int, int> maxSum(double *nums, int size) {
        double pre = nums[0];
        double maxSum = nums[0];
        int maxLeft = 0, maxRight = 0;
        int left, right;
        for(int i = 0; i < size; i++) {
            if(pre + nums[i] > nums[i]) {
                pre = pre + nums[i];
                maxRight = i;
            }else {
                pre = nums[i];
                maxLeft = i;
                maxRight = i;
            }
            if(maxSum < pre) {
                maxSum = pre;
                left = maxLeft;
                right = maxRight;
            }
        }
        return make_pair(left, right);
    }

};


int main() {
    Solution solution;
    int _size = 12;
    double _nums[] = {1.5, -12.3,3.2,-5.5,23.2,-1.4,-12.2,34.2,5.4,-7.8,1.1,-4.9};

    auto res = solution.maxSum(_nums,_size);
    cout << res.first <<" " <<res.second <<endl;

}

  

算法时间复杂度：\(O(N)\)

1.4关于排序的讨论

根据时间复杂度，排序算法大致可以分为两类

复杂度为\(O(N^2)\)的算法
复杂度为\(O(NlogN)\)的算法

关键要掌握两个计算机科学的精髓

递归
分治

假定序列有N个元素，存在于一个数组a[N]中，将数组从小到大排序。

选择排序

思想：

每一次循环从序列中挑出一个最大值，放在序列的最后，重复以上步骤，直至元素遍历完毕。

算法步骤：

从头到尾比较相邻的两个元素a[i]和a[i+1]
如果a[i]大于a[i+1]，则元素互换
从头到倒数第二个元素，重复上述过程，直至排序完成

代码实现：

#include <iostream>
#include <vector>
using namespace std;

class Solution{
public:
   vector<int> SelectionSort(vector<int> nums){
       int size = nums.size();
       for(int i = 0; i < size; i++) {
           for(int j = i + 1; j < size; j++) {
               if(nums[i] > nums[j]) {
                   int temp = nums[i];
                   nums[i] = nums[j];
                   nums[j] = temp;
               }
           }
       }
       return nums;
    }
};


int main() {
    Solution solution;
    vector<int> _nums = {3, 5, 10, 4, 2, 1, 9, 6};
    auto res = solution.SelectionSort(_nums);
    for(int i = 0; i < res.size();i++) {
        cout << res[i] << " ";
    }
    cout << endl;
}
  

算法时间复杂度：\(O(N^2)\)

插入排序

思想：

从后往前扫描，对于每一个元素，找到相应的位置插入。重复上述步骤，直至元素遍历完毕。

算法步骤：、

从第一个元素开始，该元素可以认为已经被排序
遍历数组（第一层循环），在已排序的序列中从后往前扫描（第二层循环）
若扫描的的元素大于当前遍历元素，则将扫描元素后移
直至找到已排序的元素小于或者等于当前遍历元素
将遍历元素插入到当前位置

代码实现：

#include <iostream>
#include <vector>
using namespace std;

class Solution{
public:
   vector<int> InsertSort(vector<int> nums){
       int size = nums.size();
       int i, j;
       for(i = 0; i < size; i++) {
           int temp = nums[i];
           for(j = i; j > 0 && nums[j - 1] > temp; j--) {
               nums[j] = nums[j - 1];
           }
           nums[j] = temp;
       }
       return nums;
    }
};


int main() {
    Solution solution;
    vector<int> _nums = {3, 5, 10, 4, 2, 1, 9, 6};
    auto res = solution.InsertSort(_nums);
    for(int i = 0; i < res.size();i++) {
        cout << res[i] << " ";
    }
    cout << endl;
}
  

算法时间复杂度：\(O(N^2)\)

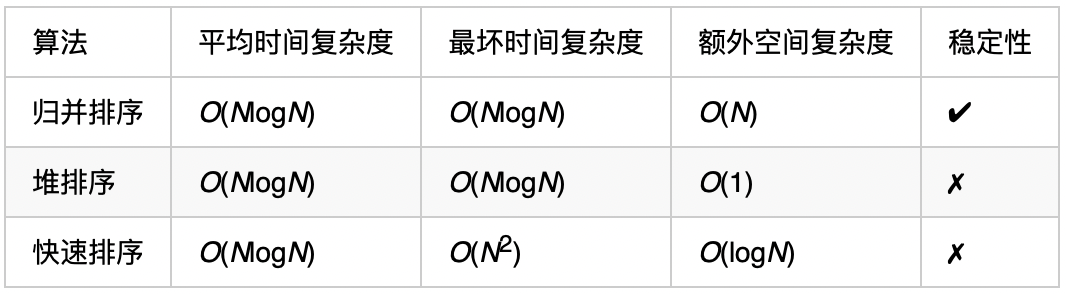
归并排序

思想：

分而治之。

算法步骤：、

假设前后两部分都是排好序的
指定两个指针,每次选择相对小的元素放入合并区间，并移动指针
重复直至某一指针到达结尾
将另一序列的剩余元素合并到序列

代码实现：

#include <iostream>
#include <vector>
#include <limits>
using namespace std;

class Solution{
public:
    void Merge(vector<int> &nums, int start, int mid, int end) {
        vector<int> leftNums(nums.begin() + start, nums.begin() + mid + 1);
        vector<int> rightNums(nums.begin() + mid + 1, nums.begin() + end + 1);
        int idxLeft = 0, idxRight = 0;
        leftNums.insert(leftNums.end(), numeric_limits<int>::max());
        rightNums.insert(rightNums.end(), numeric_limits<int>::max());

        for (int i = start; i <= end; i++) {
            if (leftNums[idxLeft] < rightNums[idxRight]) {
                nums[i] = leftNums[idxLeft];
                idxLeft++;
            } else {
                nums[i] = rightNums[idxRight];
                idxRight++;
            }
        }
    }

    void MergeSort(vector<int> &nums, int start, int end) {
        if (start >= end)
            return;
        int mid = (start + end) / 2;
        MergeSort(nums, start, mid);
        MergeSort(nums, mid + 1, end);
        Merge(nums, start, mid, end);
    }
};


int main() {
    Solution solution;
    vector<int> _nums = {3, 5, 10, 4, 2, 1, 9, 6};
    int len = _nums.size();
    solution.MergeSort(_nums, 0, len - 1);
    for(int i = 0; i < _nums.size();i++) {
        cout << _nums[i] << " ";
    }
    cout << endl;
}
  

算法时间复杂度：\(O(NlogN)\)

快速排序

思想：

分而治之思想在排序算法上的典型应用。

本质上来看，快速排序应该算是在冒泡排序基础上的递归分治法。

算法步骤：、

选择一个基准
分区操作：遍历元素，将比基准小的元素放前面，比基准大的元素放后面
递归把分区的两个序列排序

代码实现：

#include <iostream>
#include <vector>
using namespace std;

class Solution{
public:
    int Paritition(vector<int> &nums, int low, int high) {
        int pivot = nums[low];
        while (low < high) {
            while (low < high && nums[high] >= pivot) {
                --high;
            }
            nums[low] = nums[high];
            while (low < high && nums[low] <= pivot) {
                ++low;
            }
            nums[high] = nums[low];
        }
        nums[low] = pivot;
        return low;
    }

    void QuickSort(vector<int> &nums, int low, int high)
    {
        if (low < high) {
            int pivot = Paritition(nums, low, high);
            QuickSort(nums, low, pivot - 1);
            QuickSort(nums, pivot + 1, high);
        }
    }
};


int main() {
    Solution solution;
    vector<int> _nums = {3, 5, 10, 4, 2, 1, 9, 6};
    int len = _nums.size();
    solution.QuickSort(_nums, 0, len - 1);
    for(int i = 0; i < _nums.size();i++) {
        cout << _nums[i] << " ";
    }
    cout << endl;
}
  

算法时间复杂度：\(O(NlogN)\)

排序改进

今天人们对排序算法的改进大多是结合几种排序算法的思想，形成混合排序算法（Hybrid Sorting Algorithm），

将快速排序和堆排序结合起来的内省排序（Introspective Sort，简称Introsort），它成为如今大多数标准函数库（STL）中的排序函数使用的算法。
蒂姆排序（Timsort），它是今天Java和安卓（Android）操作系统内部使用的排序算法。

蒂姆排序

思想： 看成以块为单位的归并排序，块内部元素是排好序的。利用数据内部可能含有多个递增或递减的序列特性来减少排序中的比较和数据移动。

算法步骤：

找出序列中各个递增和递减的子序列
- 如果这样的子序列太短，小于一个预先设定的常数（通常是32或者64），则用简单的插入排序将它们整理为有序的子序列（也称块，run）。
- 在寻找插入位置时，该算法采用了二分查找。
- 随后将这些有序子序列一个一个放入一个临时的存储空间（堆栈）中。
按照规则合并这些块。合并的过程是先合并两个最短的，而不是一长一短地合并，可以证明这样效率会高些。

优势：

非常灵活地利用了插入排序简单直观以及归并排序效率高的特点，并且找到了归并排序的一些可以进一步提高的地方，即归并过程中过多地一对一比较大小。

排序算法的复杂度

排序算法的复杂度不可能小于O(NlogN)

N个元素的数组能排出多少种可能的序列呢？显然是N!种。因此要区分出这么多种序列的大小，挑出最小的一个，至少需要logN!次比较。

计算logN!需要使用斯特林（Stirling）公式，即lnN!=NlnN−N+O(lnN)。因此我们可以得出logN!=O(NlogN)的结论

总结

20220903002425-2022-09-03-00-24-26

总结及例题

1.1 算法的规范化和量化度量

1.2 大数和数量级的概念

例题1.1

例题1.2

例题1.3

1.4关于排序的讨论

选择排序

插入排序

归并排序

快速排序

排序改进

蒂姆排序

排序算法的复杂度

总结

1.1　算法的规范化和量化度量