信息的表示与处理

内容大纲

信息的表示与处理-2021-12-17-21-45-43

信息的存储

十六进制表示法

  • 1个字节(byte)等于8个位(bit)
  • 为什么采用16进制描述位模式，因为二进制表示法太冗长，而十进制表示法与位模式的转化很麻烦
  • C语言中，以0x或0X开头的数字常量被认为是十六进制的值
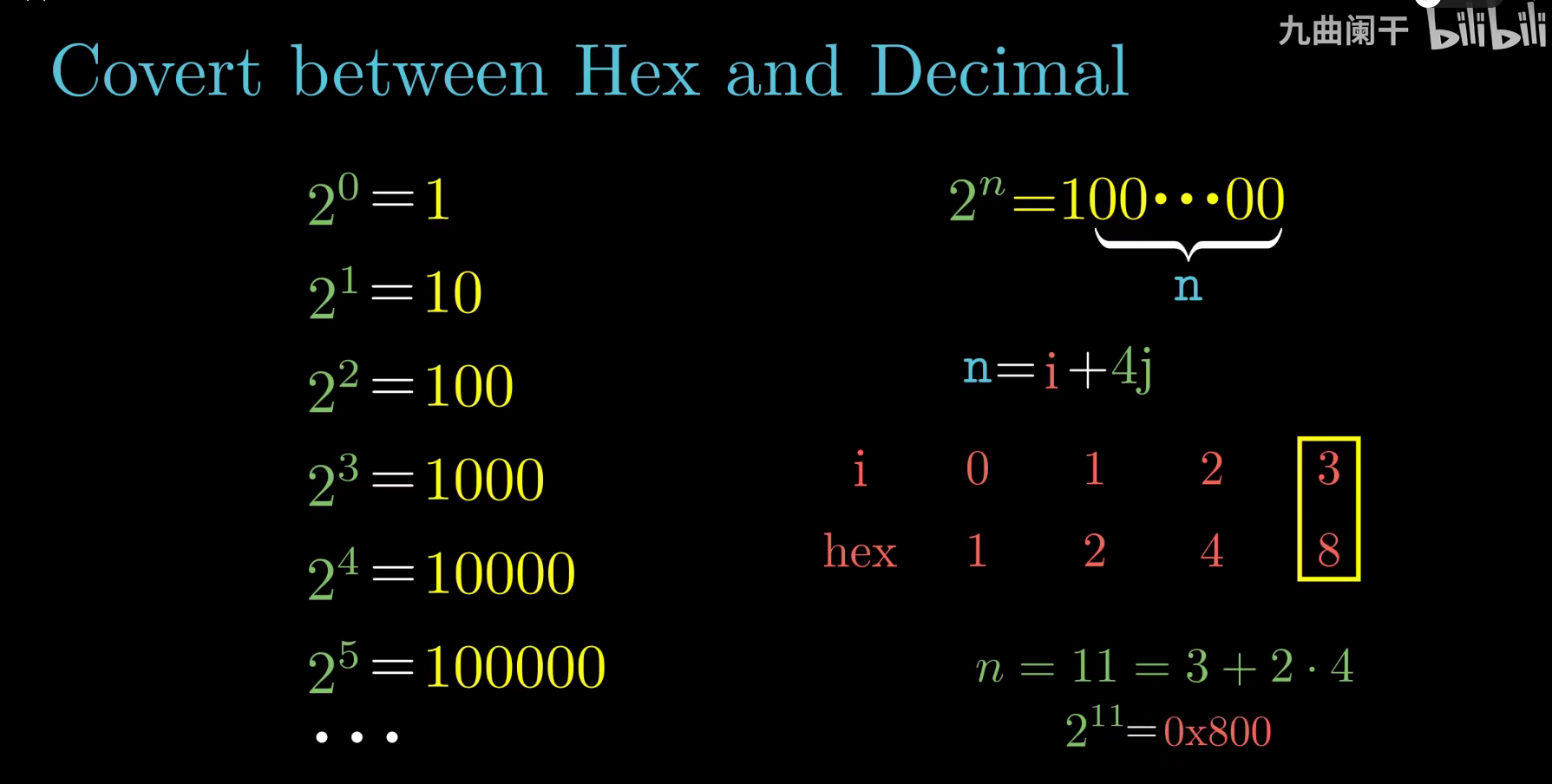
  • 数值转换 20211214163154-2021-12-14-16-31-55

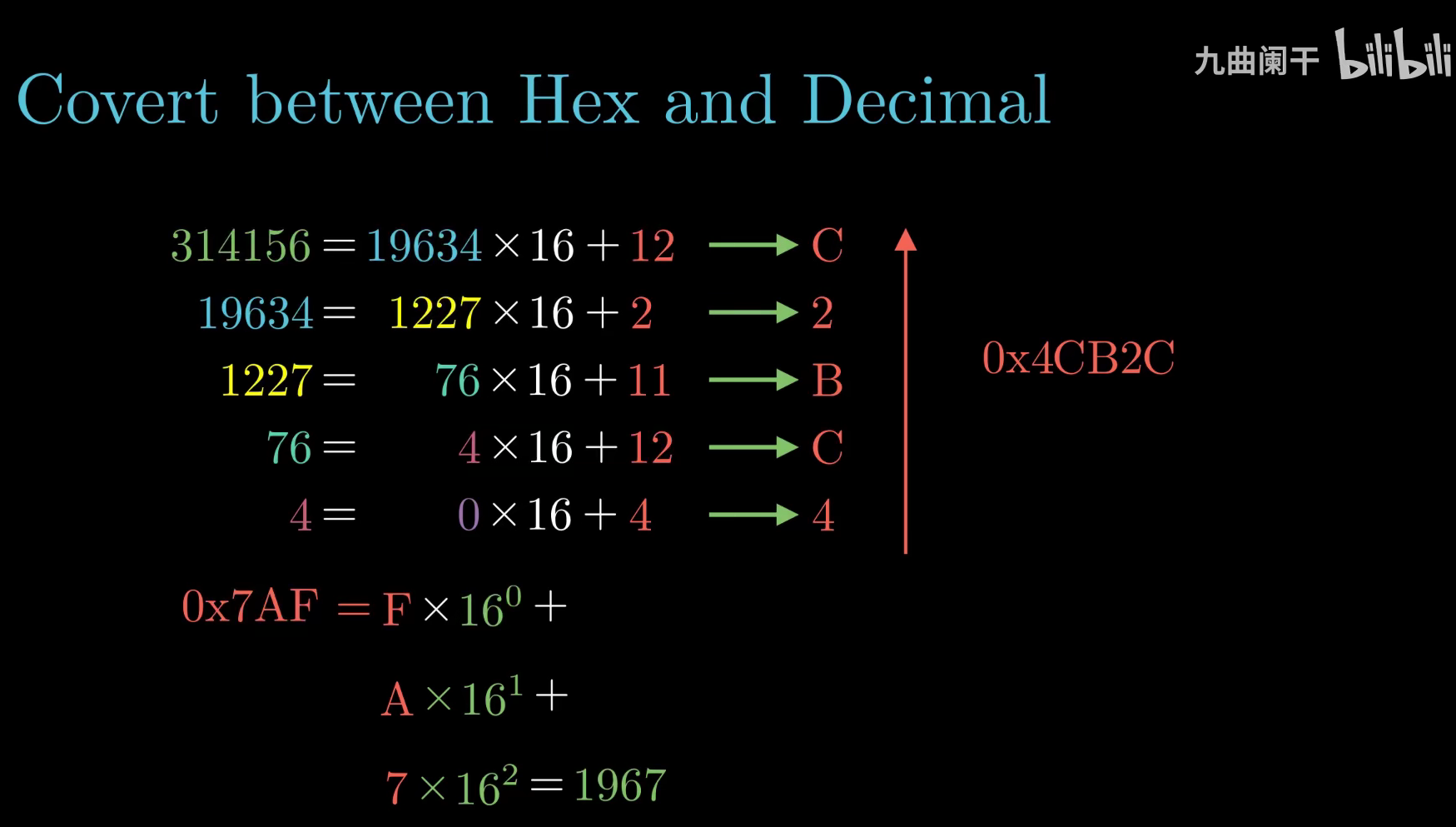
20211214165356-2021-12-14-16-53-58

字数据大小

  • 字长决定了虚拟地址空间的最大的可以到多少，也就是说，对于一个字长为 w 位的机器，虚拟地址的范围是 0 到 2^w - 1。
  • 近些年，高性能服务器、个人电脑以及智能手机已经完成了从 32 位字长到 64位字长迁移。不过在一些嵌入式的应用场景中，32 位的机器仍旧占有一席之地。对于 32 位的机器，虚拟地址空间最大为 4GB，而 64 位的机器，虚拟地址空间最大为 16EB。
  • 在迁移的过程中，大多数 64 位的机器做了向后兼容，因此为 32 位机器编译的程序也可以运行在 64 位机器上。在 64 位的机器上，可以通过这条命令编译生成可以在 32 位机器上运行的程序
  • 对于 32 位程序和 64 位程序，主要的区别还是在于程序是如何编译的，而不是运行机器的类型
  • hello32 既可以运行在 32 位机器上，也可以运行在 64 位机器上，但是 hello64 只能运行在64 位的机器上

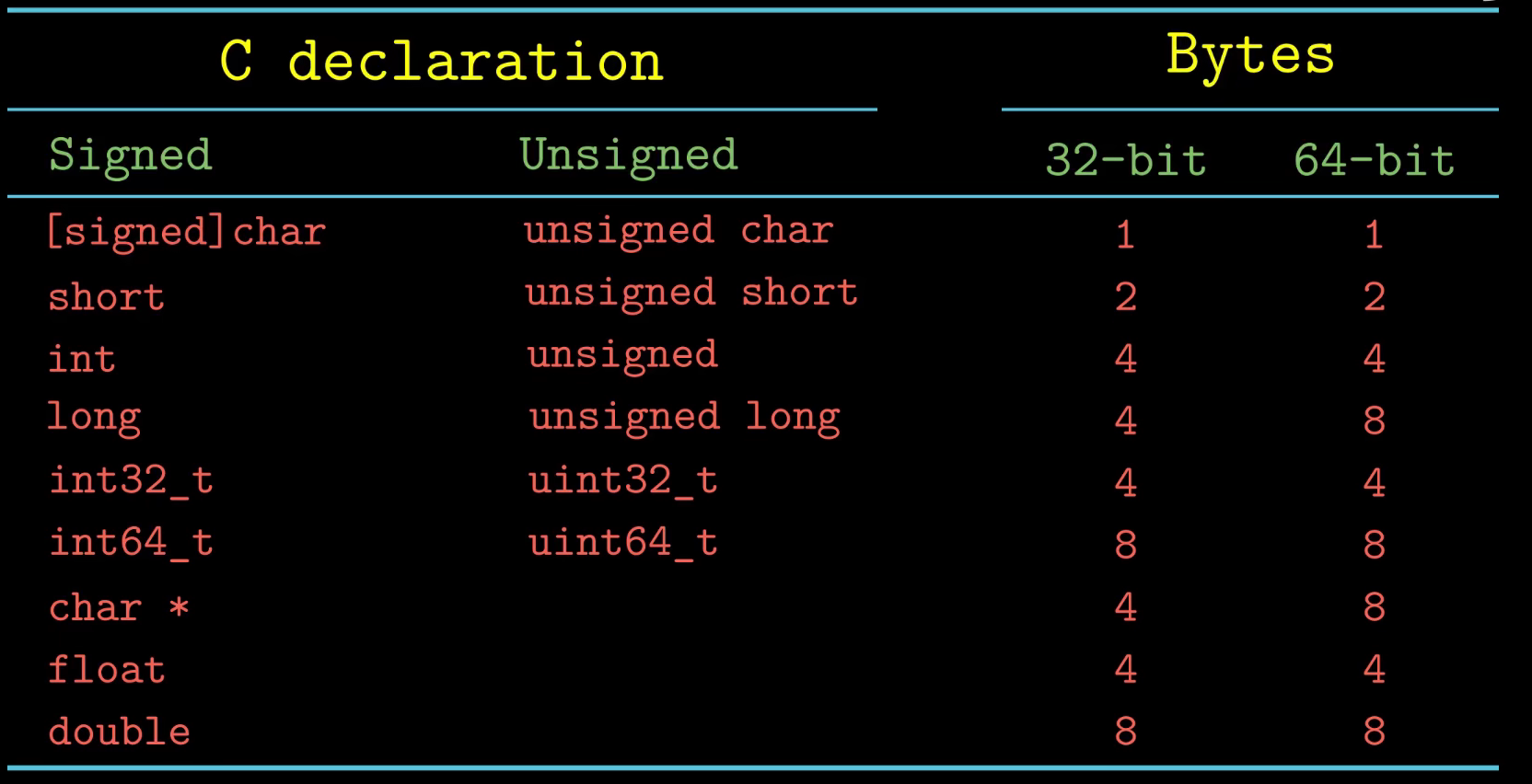
20211214171408-2021-12-14-17-14-09

寻址和字节顺序

排序一个对象的字节有两个通用的规则

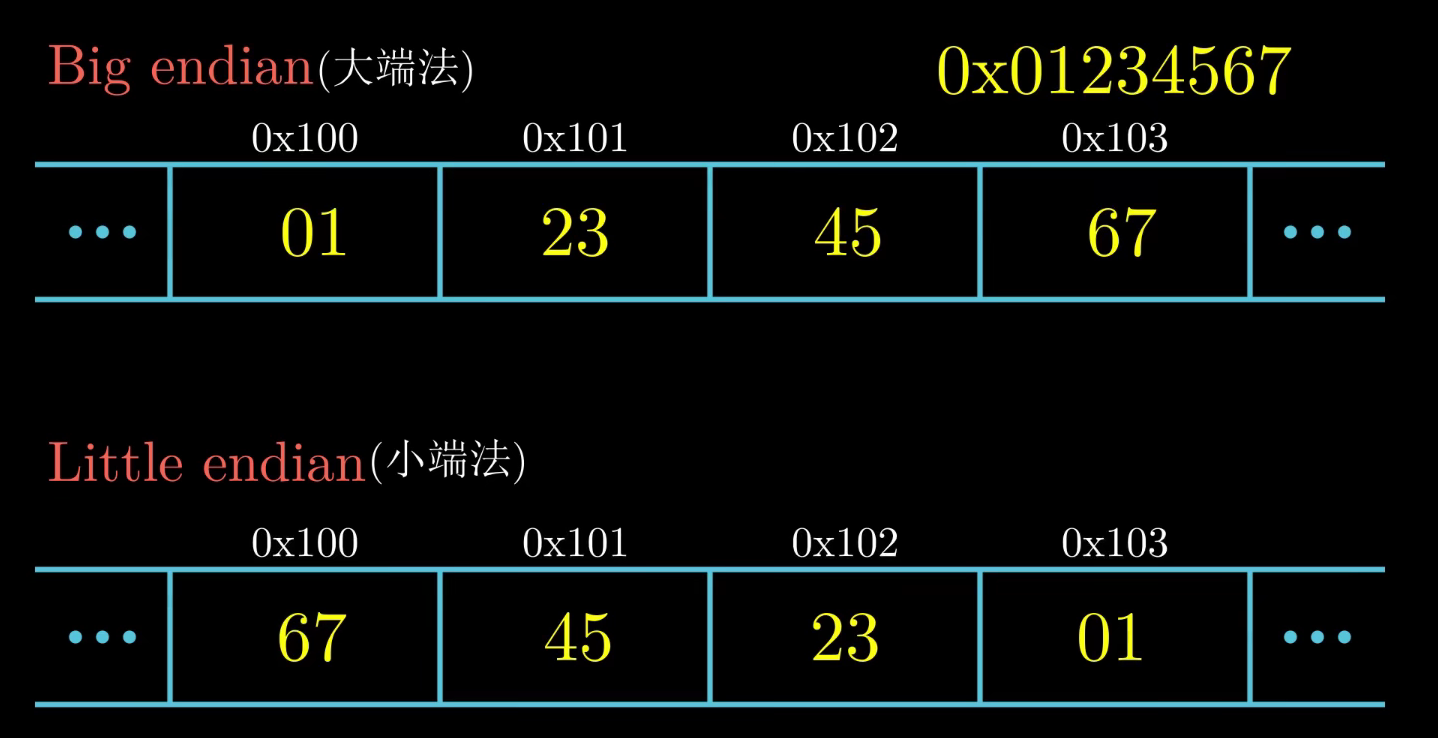
  • 大端法（最高有效字节在最前面）与小端法（最低有效字节在最前面） 20211214171613-2021-12-14-17-16-14

表示字符串

  • C 语言中的字符串被编码为以 NULL 字符结尾的字符数组，例如字符串"abcde" ，这个字符串虽然只有 5 个字符，但是长度却为 6，就是因为结尾字符的存在。

通过以下程序可以得到每个字符在内存中对应的存储信息

1 #include<stdio.h>
2 typedef unsigned char *byte_pointer;
3 void show_bytes(byte_pointer start, int len){
4 int i;
5 for(i = 0; i < len; i++){
6 printf(" %.2x", start[i]);
7 }
8 printf("\n");
9 }
10
11 void show_int(int x){
12 show_bytes((byte pointer) &x,sizeof(×));
13 }

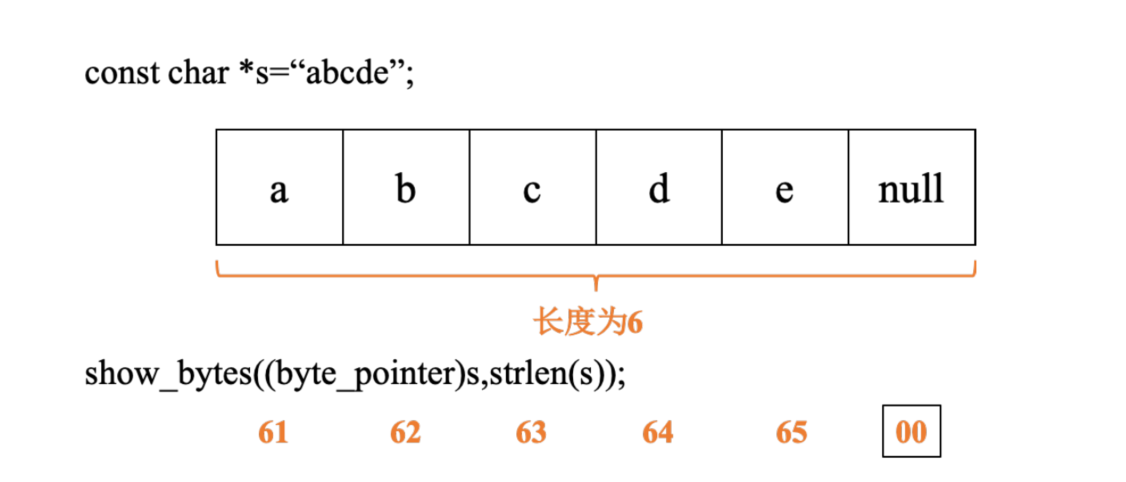
20211214173222-2021-12-14-17-32-23

  • 其中结尾字符的十六进制表示为 0x00，使用 ASCII 码来表示字符，在任何系统上都会得到相同的结果。因此，文本数据比二进制数据具有更强的平台独立性。

布尔代数

布尔运算

  • 布尔运算~对应逻辑运算NOT
  • 布尔运算&对应逻辑运算AND
  • 布尔运算|对应逻辑运算OR
  • 布尔运算^对应逻辑运算异或 20211214173355-2021-12-14-17-33-55

C语言中的位级运算

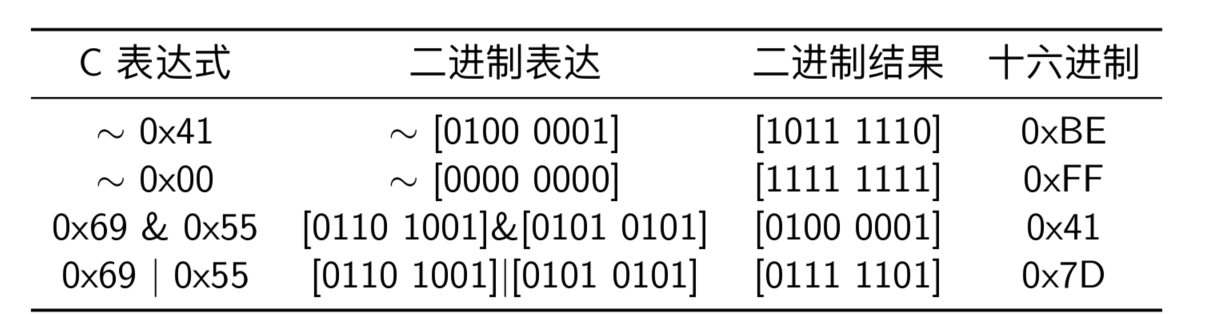
  • C 语言中的一个特性就是支持按位进行布尔运算，确定一个位级表达式结果的最好方法，就是将十六进制扩展成二进制表示，然后按位进行相应的运算，最后再转换回十六进制 20211214181106-2021-12-14-18-11-07
  • 位运算一个常见的用法就是实现掩码运算，通俗点讲，通过位运算可以得到特定的位序列。例如对于操作数 0x89ABCDEF，我们想要得到该操作数的最低有效字节的值，可以通过 & 0xFF，这样我们就得到了最低有效字节 0x0000 00EF

C 语言中的逻辑运算

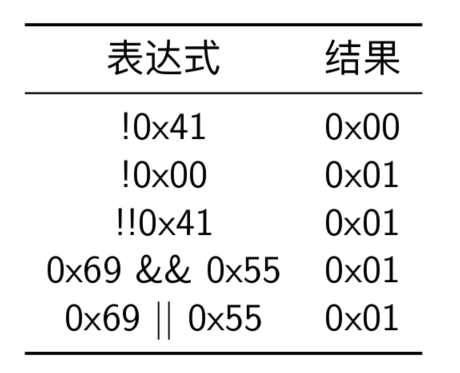
  • 除了位级运算之外，C 语言还提供了一组逻辑运算，注意逻辑运算的运算符与位级运算容易混淆。逻辑运算认为所有非零的参数都表示 true，只有参数 0 表示 false 20211214181752-2021-12-14-18-17-53
  • 对于 if(a && 5/a) 表达式，如果 a 等于 0，该逻辑运算的结果即为 false，不用再去计算 5 除以 a，这样就可以避免了出现 5 除以 0 的情况

C语言中的移位运算

  • C语言提供了一组移位运算，向左或向右移动位模式
  • x向左移动k位，丢弃最高的k位，在右端补k个0
  • 右移分为两种
    • 逻辑右移， 在左端补k个0
    • 算术右移，在左端补k个最高有效位的值
左操作 正数 负数
参数x [001100011] [10010101]
x « 4 [00110000] [01010000]
x « 4(逻辑右移) [00000110] [00001001]
x « 4（算术右移） [00000110] [11111001]

整数表示

有符号的二进制数的表示

十进制数有正负之分，那么二进制数也有正负之分。带有正、负号的二进制数称为真值，例如 +1010110、-0110101 就是真值。为了方便运算，在计算机中约定: 在有符号数的前面增加 1 位符号位，用 0 表示正号，用 1 表示负号。这种在计算机中用0 和 1 表示正负号的数称为机器数。目前常用的机器数编码方法有原码、反码和补码 3 种。

  1. 原码
    • 正数的符号位用"0"表示，负数的符号位用"1"表示，其余数位表示数值本身
    • 例如:X=+1010110, $[X]_原$ =01010110
    • Y=-0110101, $[Y]_原$ =10110101
    • 用原码表示的数在计算机中进行加减法运算很麻烦。比如遇到两个异号数相加或者两个同号数相减时，就要做减法。为了简化运算器的复杂性，提高运算速度，需要把减法做成加法运算，因此人们引入了反码和补码
  2. 反码
    • 正数的反码与其原码相同; 负数的反码是在原码的基础上保持符号位不变，其余各位按位求反得到的
    • 例如:X=+1010110, $[X]_反$ =$[X]_原$ =01010110.
    • Y=-0110101, $[Y]_原$ =10110101 $[Y]_反$ =11001010
  3. 补码
    • 正数的补码与其原码相同; 负数的补码是在原码的基础上保持符号位不变，其它的数位 1 变为 0，0 变为 1，最后再加 1 运算
    • 在计算机中，有符号整数常常用补码形式存储
    • 对于任意一个数它的补码的补码是原码，即 [[X]补]补 =[X]原
    • 例如:X=+1010110 [X] 补 =[X] 反 =[X] 原 =01010110
    • Y=-0110101 [Y] 原 =10110101 [Y] 补 =11001011
    • 补码中 0 无正负之分，即 [+0]补 =[-0]补 =00000000

整数运算

有符号数和无符号数转换

  • C 语言允许数据类型之间做强制类型转换
    • 有符号转无符号 20211214204420-2021-12-14-20-44-21
    • 无符号转有符号 20211214205001-2021-12-14-20-50-02
    • 在 C 语言中，在执行一个运算时，如果一个运算数是有符号数，另外一个运算数是无符号数，那么 C 语言会隐式的将有符号数强制转换成无符号数来执行运算 
      1 int i = -1;
2 unsigned int b = 0;
3 if(a < b)
4 printf("−1 < 0")
5 else
6 printf("−1 > 0")
    • 输出-1>0，由于第二个操作数 b 是无符号数，第一个操作数 a 就隐式的转换成无符号数，这个表达式实际上比较的是 4294967295(=2^32 − 1) < 0
    • C 语言中将一个较小数据类型转换成较大的类型时，保持数值不变是可以的；但大转小不行
    • 转换定理：当有符号数从一个较小的数据类型转换成较大类型时，进行符号位扩展，可以保持数值不变
  • 截断
    • 将int类型强制类型转换成short类型时，int 类型高16位数据被丢弃，留下低 16位的数据，因此截断一个数字，可能会改变它原来的数值
      • 无符号数：
        • 将一个 w 位的无符号数，截断成 k 位时，丢弃最高的 w-k 位，截断操作可以对应于取模运算，即除以 2 的 k 次方之后得到的余数。
      • 有符号数：
        • 我们用无符号数的函数映射来解释底层的二进制位，这样一来我们就可以使用与无符号数相同的截断方式，得到最低 K 位；
        • 我们将第一步得到的无符号数转换成有符号数

无符号加法

  • 在 C 语言执行的过程中，对于溢出的情况并不会报错，但是我们希望判定运算结果是否发生了溢出 
    1 int uadd_ok(unsigned x, unsigned y){
2 unsigned sum = x + y;
3 return sum >= x; // 溢 出 返 回 0， 没 溢 出 返 回 1
4 }
因为 x 和 y 都是大于 0 的，因此，两者之和大于其中任何一个

    补码加法

    与无符号数相加不同的是，有符号数的溢出分为正溢出和负溢出。

  • 当 x 加 y 的和大于等于 $2^{w-1}$ 时，发生正溢出，此时，得到的结果会减去 $2^w$
  • 当 x 加 y 的和小于 $-2^{w-1}$时，发生负溢出，此时，得到的结果会加上 $2^w$

乘法运算

  1. 无符号数乘法
    • w 位的无符号数 x 和 y，二者的乘积可能需要 2w 位来表示。在 C 语言中，定义了无符号数乘法所产生的结果是 w 位，因此，运行结果会截取 2w 位中的低 w 位。截断采用取模的方式，因此，运行结果等于 x 与 y 乘积并对 2 的 w 次方取模
  2. 补码乘法
    • 计算机的有符号数用补码表示，因此补码乘法就是有符号数乘法。无论是无符号数乘法，还是补码乘法，运算结果的位级表示都是一样的，只不过补码乘法比无符号数乘法多一步，需要将无符号数转换成补码（有符号数）。虽然完整的乘积结果的位级表示可能会不同，但是截断后的位级表示都是相同的
    • 其它一些情况，如果乘以的是 2 的整数倍，那么可以通过位移进行快速运算

除法运算

我们以乘除 2 的倍数为例进行讨论补码乘除的运算规则:

  • 原码运算：
    • 对于一般的以 $2^w$ 为因子的乘法，我们只需要对原码进行移动，例如:$[5]_原$ =0101 ，若将原码乘以 2，则相当于所有位数向左移动一个单位，即为 1010 =$[10]_原$ ，除法只需要进行右移即可。即: 对于原码，不论正负，若某个数字乘 $2^w$的倍数，则只需要对原码向左移动 w 个单位，空缺位补 0。

浮点数

IEEE浮点表示

V = $(-1)^s$ × M × $2^E$

  • 三个变量：符号 s、阶码 E 和尾数 M，下面以单精度浮点数为例。
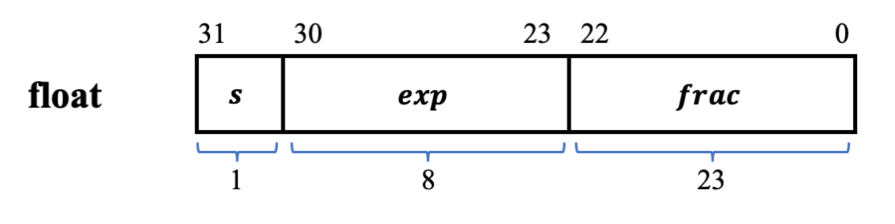
  • 例如 C 语言中 float 类型的变量占 4 个字节，32 个比特位，这 32 个比特位被划分成 3 个字段来解释 20211215135840-2021-12-15-13-58-41

    • 其中最高位 31 位表示符号位 s。当 s=0 时，表示正数；s=1 时则表示负数。从第23 位到 30 位，这 8 个二进制位与阶码的值 E 是相关的。剩余的 23 位与尾数 M 是相关的 20211215140350-2021-12-15-14-03-51

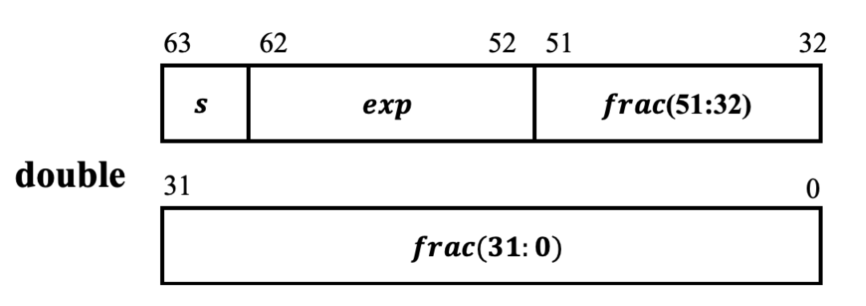
    • 对于 64 位双精度浮点数，其二进制位与浮点数的关系如图所示 20211215160635-2021-12-15-16-06-36

  • 与单精度浮点数相比，双精度浮点数的符号位也是 1 位。但是阶码字段的长度为 11位，小数字段的长度为 52 位

  • 浮点数的数值可以分为三类，其中阶码的值决定了这个数是属于其中哪一类
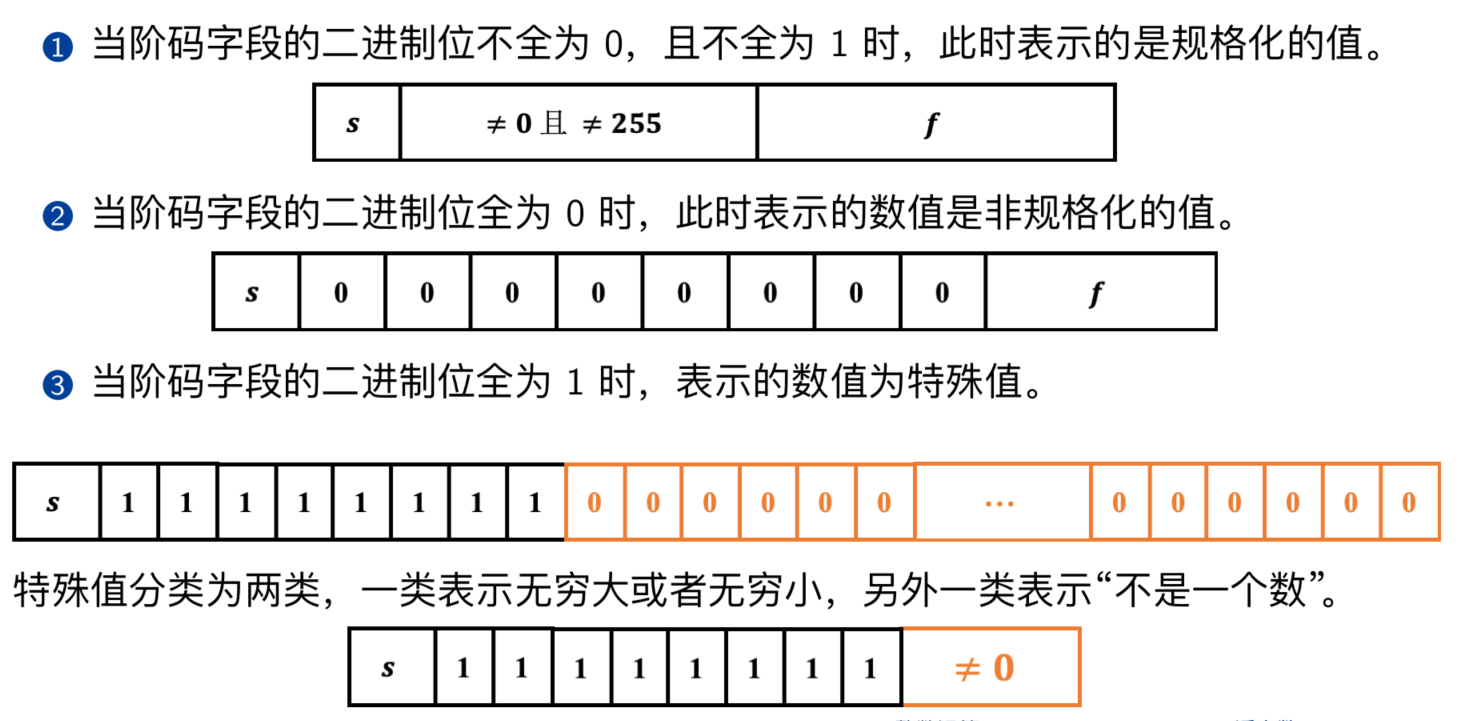
    • 规格化的值。当阶码字段的二进制位不全为 0，且不全为 1 时
      • 当表示单精度的值时，阶码字段的长度为 8，偏置量等于 127
        • bias(float)=$2^{8 - 1}$−1=127
      • 当表示双精度的数时，阶码字段的长度为 11，偏置量等于 1023
        • bias(double)=$2^{11−1}$ -1=1023
    • 非规格化的值，当阶码字段的二进制位全为 0,主要有两个用途
      • 提供了表示数值 0 的方法，当符号位 s 等于 0，阶码字段全为 0，小数字段也全为 0 时，此时表示正零。当符号位 s 等于 1，阶码字段全为 0，小数字段也全为 0 时，此时表示负零。根据 IEEE 的浮点规则，正零和负零在某些方面被认为不同，而其他方面是相同的
      • 非规格化的数是可以表示非常接近 0 的数。当阶码字段全为 0 的时，阶码 E 的值等于 1-bias，而尾数的值 M 等于 f，不包含隐藏的 1。这与规格化的值的解释方法不同，需要特别注意 20211215165018-2021-12-15-16-50-19
    • 特殊值，当阶码字段的二进制位全为 1 时，表示的数组为特殊值。特殊值分类为两类，一类表示无穷大或者无穷小，另外一类表示"不是一个数"
      • 当阶码字段全为 1，且小数字段全为 0 时，表示无穷大的数
        • 如果符号位 s 等于 0 时，表示正无穷大
        • 符号位 s 等于 1，表示负无穷大
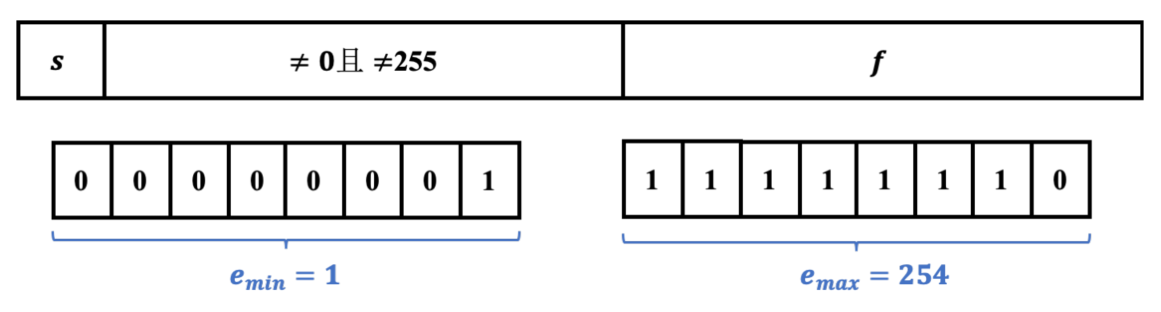
  • 当表示规格化的值时，其中阶码字段的取值范围如图所示 20211215162953-2021-12-15-16-29-54
  • 最小值是 1，最大值是 254。为了方便表述，我们用小写字母 e 来表示这个 8 位二进制数，需要注意的是阶码 E 的值并不等于 e (8 个二进制位) 所表示的值，而是 e的值减去一个偏置量，偏置量的值与阶码字段的位数是相关的
E = e − bias

整型转单精度浮点型

根据我们 IEEE 浮点数的编码规则，我们将小数点左边的 1 丢弃，由于单精度的小数字段长度为 23，我们还需要在末端增加 10 个零：

  • 1 0000 0011 1001 0000 0000 00 这样我们就得到了浮点数的小数字段，从 12345 的规格化表示可以发现阶码 E 的值等于 13，由于单精度浮点数的 bias 等于 127，因此根据公式 E=e-bias，可以计算出 e 的值等于 140，其二进制表示如下：
  • E = e − bias
  • e=140 1000 1100 这样一来，得到了浮点数的阶码字段，再加上符号位的 0，整个单精度浮点数的二进制表示就构造完毕 20211215171420-2021-12-15-17-14-21 由于表示方法的原因，限制了浮点数的范围和精度，所以浮点运算只能近似的表示实数运算

舍入

IEEE 浮点格式定义了四种不同的舍入方式，分别是：向偶数舍入、向零舍入、向下舍入以及向上舍入

  • 向下舍入总是朝向小的方向进行舍入
  • 向上舍入总是朝向大的方向进行舍入
  • 向零舍入就是把正数进行向下舍入，把负数进行向上舍入。将这种舍入规则映射到数轴上，可以发现舍入是朝向零的方向
  • 向偶数舍入，也被称为向最接近的值进行舍入，例如1.40 -> 1, -1.5 -> 2

注意事项：

  • 当遇到两个可能结果的中间数值时，舍入结果应该如何计算，向偶数舍入的结果要遵循最低有效数字是偶数的规则，因此 1.5 的舍入结果究竟 是 1 还是 2，取决于 1 和 2 哪个数是偶数.
  • 乍一看，向偶数舍入这种方式有点随意，为什么要偏向取偶数呢?
  • 如果总是采用向上舍入，会导致结果的平均值相对于真实值略高；如果总是采用向下舍入，会导致结果的平均值相对于真实值略低。向偶数舍入就避免了这 种统计偏差。使得有一半的情况需要向上舍入，有一半的情况需要向下舍入。
  • 对于不想舍入到整数的情况，向偶数舍入的方法同样适用。我们只需要考虑最低有效位是偶数还是奇数即可

浮点运算

  • C 语言提供了两种不同的浮点数据类型：单精度 float 类型和双精度 double 类型。当 int，float、double 不同数据类型之间进行强制类型转换时，得到的结果可能会超出我们的预期
  • 当 int 类型转换成 float 类型时，数字不会发生溢出，但是可能会被舍入。这是由于单精度浮点数的小数字段是 23 位，可能会出现无法保留精度的情况。
  • 从 double 类型转换成 float 类型，由于 float 类型所表示数值的范围更小，所以可能会发生溢出
  • 此外，float 类型的精度相对于 double 较小，转换后还可能被舍入。
  • 将 float 类型或者 double 类型的浮点数转换成 int 类型，一种可能的情况是值会向零舍入，例如 1.9 将被转换成 1，-1.9 将被转换成-1；另外一种可能的情况是发生溢出

参考资料

Datawhale CSAPP组队学习

CSAPP-深入理解计算机系统