环形链表II
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例:
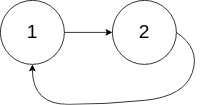
输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
思路
解法一:
使用快慢指针法先将两个指针都指向 head ,若为环,则两个指针必定相遇。
设链表中环外部分的长度为 a。slow 指针进入环后,又走了 b 的距离与 fast 相遇。此时,fast 指针已经走完了环的 n 圈,因此它走过的总距离为$ a+n(b+c)+b=a+(n+1)b+nc $。
\[a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)\]从相遇点到入环点的距离加上 n−1 圈的环长,恰好等于从链表头部到入环点的距离。
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* slow = head;
ListNode* fast = head;
while (fast != nullptr) {
slow = slow->next;
if (fast->next == nullptr) {
return nullptr;
}
fast = fast->next->next;
if (fast == slow) {
ListNode *temp = head;
while (temp != slow) {
temp = temp->next;
slow = slow->next;
}
return temp;
}
}
return nullptr;
}
};