卡尔曼滤波

什么是卡尔曼滤波？

卡尔曼滤波器就是根据上一时刻的状态，预测当前时刻的状态，将预测的状态与当前时刻的测量值进行加权，加权后的结果才认为是当前的实际状态，而不是仅仅听信当前的测量值。

对于这个滤波器，我们几乎可以下这么一个定论：只要是存在不确定信息的动态系统，卡尔曼滤波就可以对系统下一步要做什么做出有根据的推测。即便有噪声信息干扰，卡尔曼滤波通常也能很好的弄清楚究竟发生了什么，找出现象间不易察觉的相关性。

因此卡尔曼滤波非常适合不断变化的系统，它的优点还有内存占用较小（只需保留前一个状态）、速度快，是实时问题和嵌入式系统的理想选择。

能用卡尔曼滤波做什么？

让我们举个例子：你造了一个可以在树林里四处溜达的小机器人，为了让它实现导航，机器人需要知道自己所处的位置。机器人有一个包含位置信息和速度信息的状态\(\mathop{x_k}\limits ^{\rightarrow}\)。

注意，在这个例子中，状态是位置和速度，放进其他问题里，它也可以是水箱里的液体体积、汽车引擎温度、触摸板上指尖的位置，或者其他任何数据。

我们的小机器人装有GPS传感器，定位精度10米。虽然一般来说这点精度够用了，但我们希望它的定位误差能再小点，毕竟树林里到处都是土坑和陡坡，如果机器人稍稍偏了那么几米，它就有可能滚落山坡。所以GPS提供的信息还不够充分。

我们也可以预测机器人是怎么移动的：它会把指令发送给控制轮子的马达，如果这一刻它始终朝一个方向前进，没有遇到任何障碍物，那么下一刻它可能会继续坚持这个路线。但是机器人对自己的状态不是全知的：它可能会逆风行驶，轮子打滑，滚落颠簸地形……所以车轮转动次数并不能完全代表实际行驶距离，基于这个距离的预测也不完美。

这个问题下，GPS为我们提供了一些关于状态的信息，但那是间接的、不准确的；我们的预测提供了关于机器人轨迹的信息，但那也是间接的、不准确的。

但以上就是我们能够获得的全部信息，在它们的基础上，我们是否能给出一个完整预测，让它的准确度比机器人搜集的单次预测汇总更高？用了卡尔曼滤波，这个问题可以迎刃而解。

卡尔曼滤波眼里的机器人问题

还是上面这个问题，我们有一个状态，它和速度、位置有关：

我们不知道它们的实际值是多少，但掌握着一些速度和位置的可能组合，其中某些组合的可能性更高：

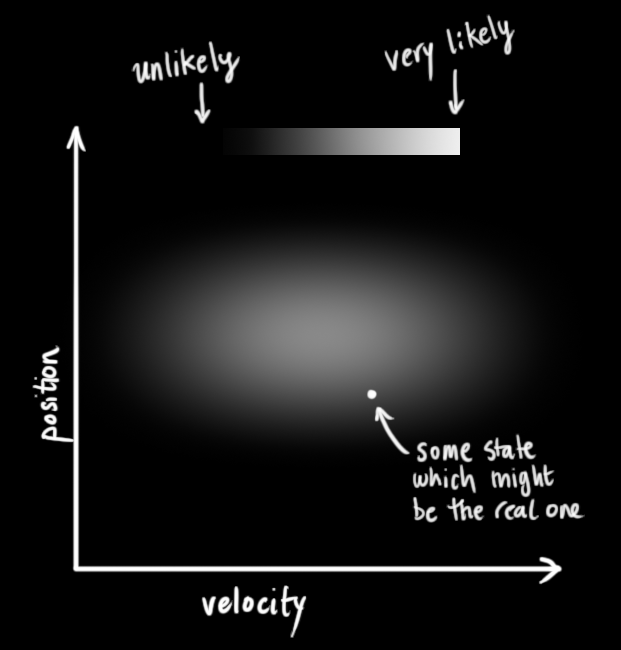
卡尔曼滤波假设两个变量（在我们的例子里是位置和速度）都应该是随机的，而且符合高斯分布。每个变量都有一个均值 \(\mu\) ，它是随机分布的中心；有一个方差 \(\sigma^2\) ，它衡量组合的不确定性。

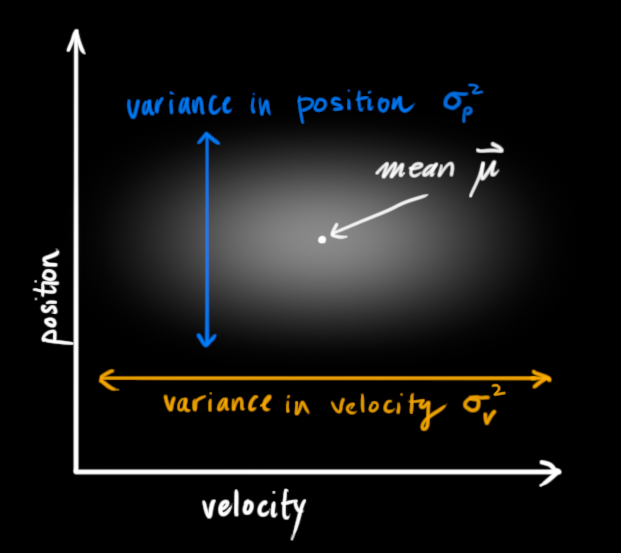
在上图中，位置和速度是不相关的，这意味着我们不能从一个变量推测另一个变量。

那么如果位置和速度相关呢？如下图所示，机器人前往特定位置的可能性取决于它拥有的速度。

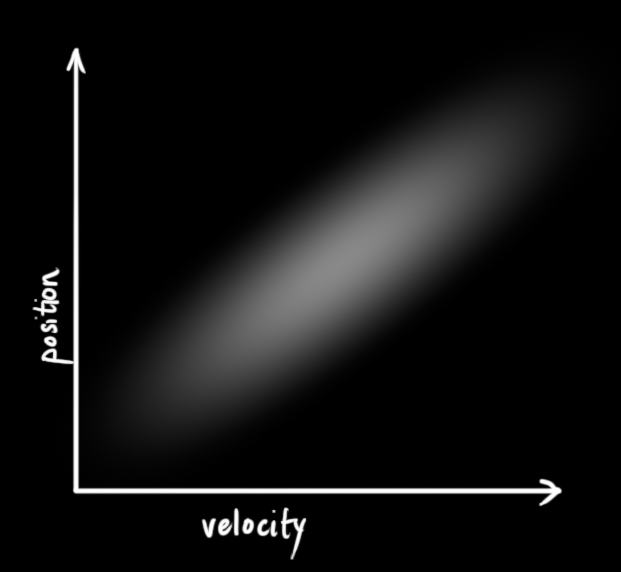
这不难理解，如果基于旧位置估计新位置，我们会产生这两个结论：如果速度很快，机器人可能移动得更远，所以得到的位置会更远；如果速度很慢，机器人就走不了那么远。

这种关系对目标跟踪来说非常重要，因为它提供了更多信息：一个可以衡量可能性的标准。这就是卡尔曼滤波的目标：从不确定信息中挤出尽可能多的信息！

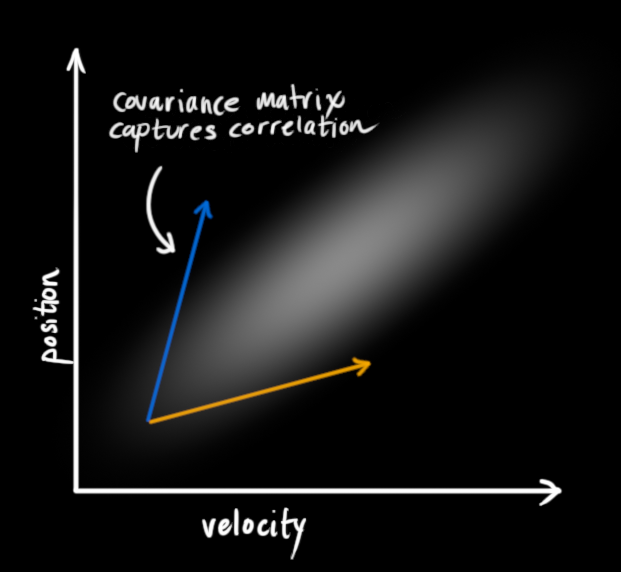
为了捕获这种相关性，我们用的是协方差矩阵。简而言之，矩阵的每个值是第 \(i\) 个变量和第 \(j\) 个变量之间的相关程度（由于矩阵是对称的， \(i\) 和 \(j\) 的位置可以随便交换）。我们用 \(\Sigma\) 表示协方差矩阵，在这个例子中，就是\(\Sigma_{ij}\)。

用矩阵描述问题

为了把以上关于状态的信息建模为高斯分布（图中色块），我们还需要 \(k\) 时的两个信息：最佳估计 \(\hat{x_k}\) （均值，也就是\(u\) ，协方差矩阵 \(P_K\) 。（虽然还是用了位置和速度两个变量，但只要和问题相关，卡尔曼滤波可以包含任意数量的变量）

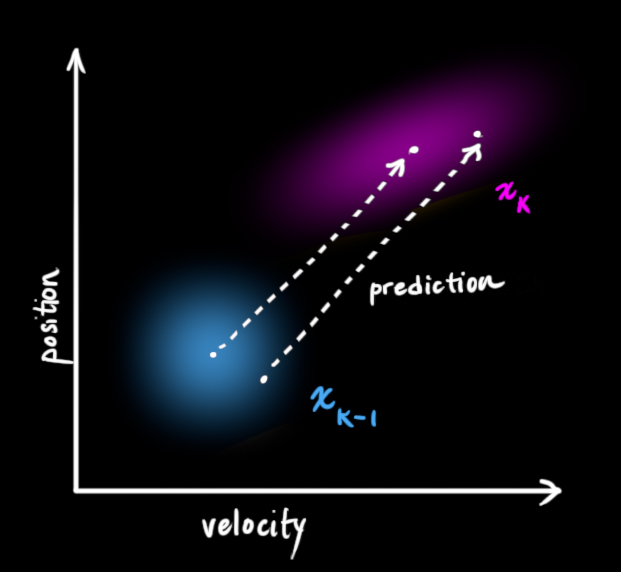
我们可以用矩阵\(F_k\)表示这个预测步骤：

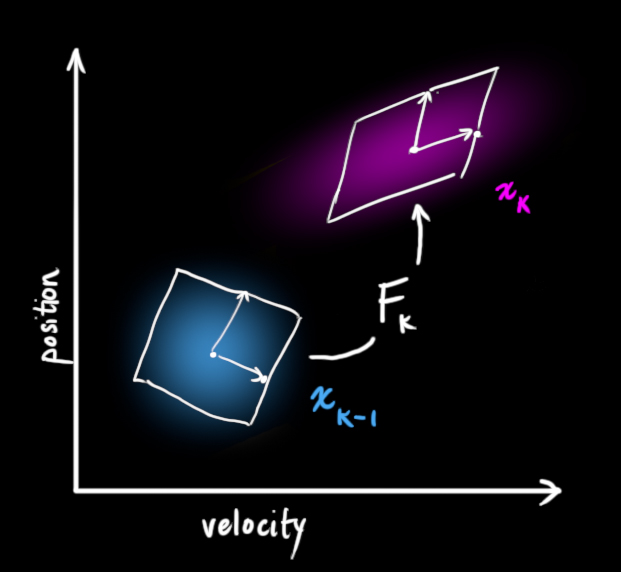
它获取我们原始估计中的每个点并将其移动到新的预测位置，如果原始估计是正确的，系统将移动到该位置。

这是怎么做到的？为什么我们可以用矩阵来预测机器人下一刻的位置和速度？下面是个简单公式：

这是一个预测矩阵，它能给出机器人的下一个状态，但目前我们还不知道协方差矩阵的更新方法。这也是我们要引出下面这个等式的原因：如果我们将分布中的每个点乘以矩阵A，那么它的协方差矩阵会发生什么变化

把这个式子和上面的最佳估计\(\hat{x}_k\)结合，可得：

外部影响

但是，除了速度和位置，外因也会对系统造成影响。比如模拟火车运动，除了列车自驾系统，列车操作员可能会手动调速。在我们的机器人示例中，导航软件也可以发出停止指令。对于这些信息，我们把它作为一个向量 \(\color{darkorange}{\vec{\mathbf{u}_k}}\) ，纳入预测系统作为修正。

假设油门设置和控制命令是已知的，我们知道火车的预期加速度 \(a\) 。根据运动学基本定理，我们可得：

矩阵形式为：

\(B_k\)是控制矩阵， \(\color{darkorange}{\vec{\mathbf{u}_k}}\)是控制向量。如果外部环境异常简单，我们可以忽略这部分内容，但是如果添加了外部影响后，模型的准确率还是上不去，这又是为什么呢？

外部不确定性

如果状态基于其自身属性而演变，那么一切都很好。如果状态在外力的基础上发展，一切都很好，那么我们知道那些外力是什么。

但是，如果存在我们不知道的力量呢？当我们监控无人机时，它可能会受到风的影响；当我们跟踪轮式机器人时，它的轮胎可能会打滑，或者粗糙地面会降低它的移速。这些因素是难以掌握的，如果出现其中的任意一种情况，预测结果就难以保障。

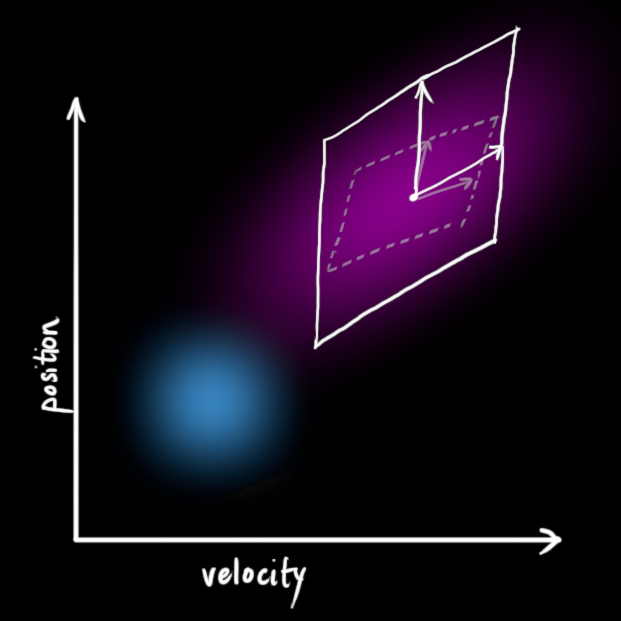
这要求我们在每个预测步骤后再加上一些新的不确定性，来模拟和"世界"相关的所有不确定性：

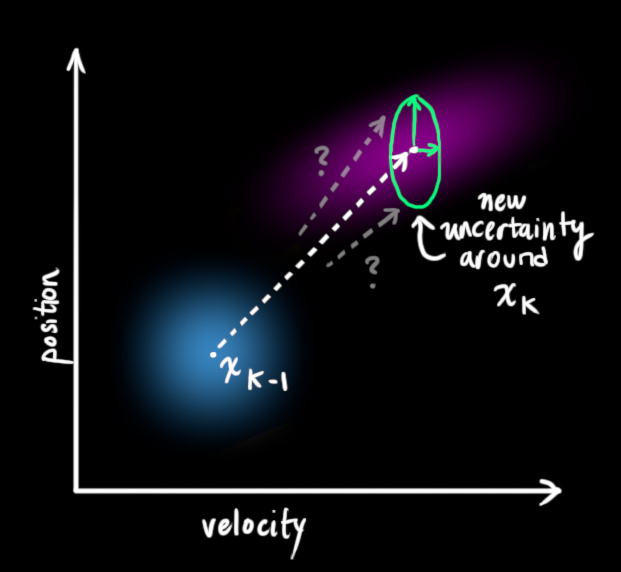
如上图所示，加上外部不确定性后，\(\color{royalblue}{\mathbf{\hat{x}}_{k-1}}\)的每个预测状态都可能会移动到另一点，也就是蓝色的高斯分布会移动到紫色高斯分布的位置，并且具有协方差\(\color{mediumaquamarine}{\mathbf{Q}_k}\)。换句话说，我们把这些不确定影响视为协方差\(\color{mediumaquamarine}{\mathbf{Q}_k}\)的噪声。

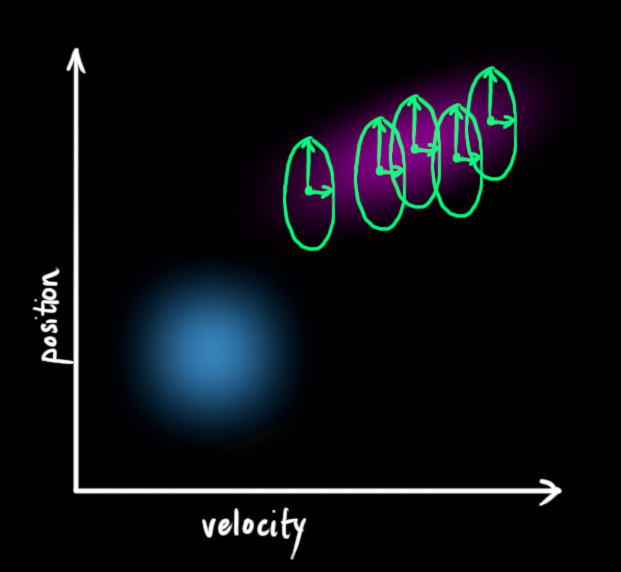
这个紫色的高斯分布拥有和原分布相同的均值，但协方差不同。

我们在原式上加入\(\color{mediumaquamarine}{\mathbf{Q}_k}\)： \(\begin{equation} \begin{split} \color{deeppink}{\mathbf{\hat{x}}_k} &= \mathbf{F}_k \color{royalblue}{\mathbf{\hat{x}}_{k-1}} + \mathbf{B}_k \color{darkorange}{\vec{\mathbf{u}_k}} \\ \color{deeppink}{\mathbf{P}_k} &= \mathbf{F_k} \color{royalblue}{\mathbf{P}_{k-1}} \mathbf{F}_k^T + \color{mediumaquamarine}{\mathbf{Q}_k} \end{split} \label{kalpredictfull} \end{equation}\)

简而言之，这里：

新的最佳估计 是基于 原最佳估计 和 已知外部影响 校正后得到的预测。

新的不确定性 是基于 原不确定性和外部环境的不确定性 得到的预测。

现在，有了这些概念介绍，我们可以把传感器数据输入其中。

通过测量来细化估计值

我们可能有好几个传感器，它们一起提供有关系统状态的信息。传感器的作用不是我们关心的重点，它可以读取位置，可以读取速度，重点是，它能告诉我们关于状态的间接信息——它是状态下产生的一组读数。

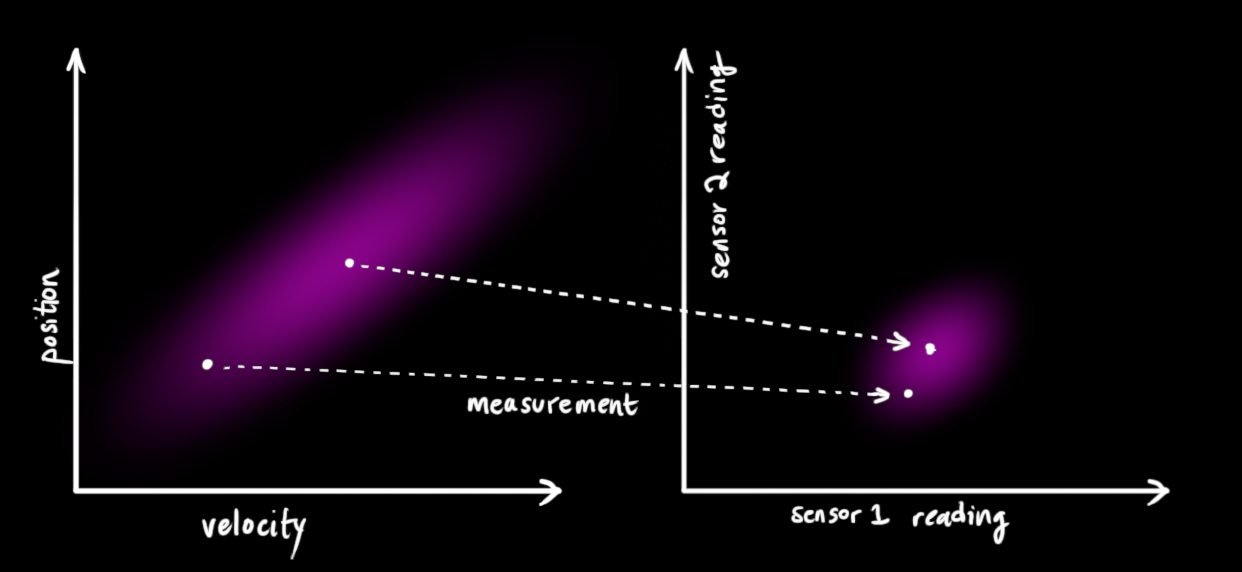
请注意，读数的规模和状态的规模不一定相同，所以我们把传感器读数矩阵设为\(H_k\) 。

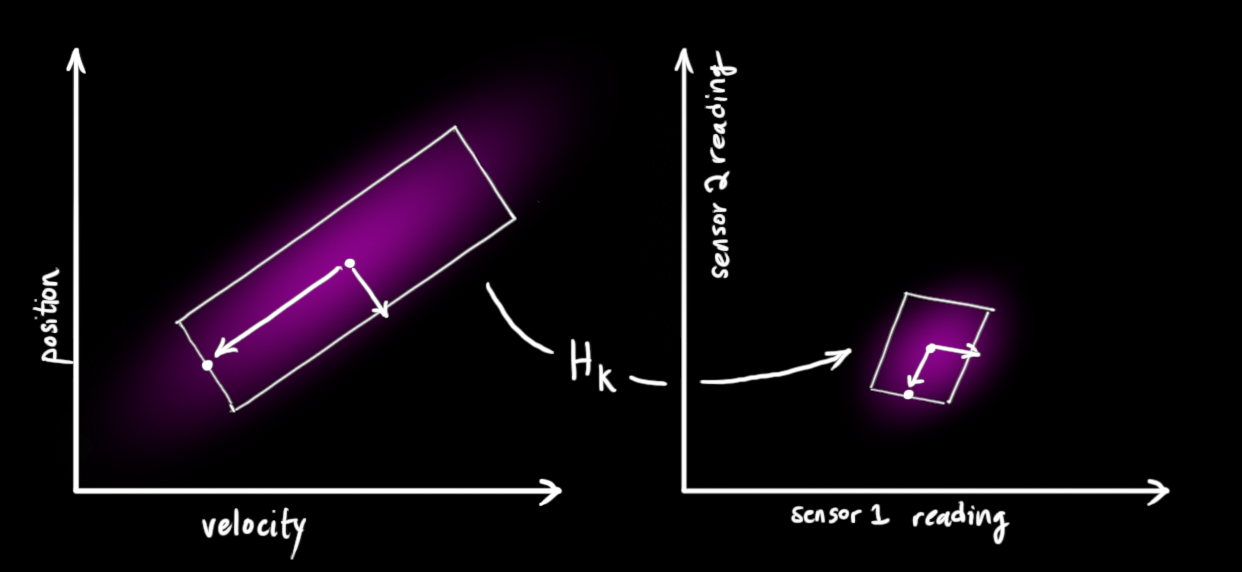
把这些分布转换为一般形式： \(\begin{equation} \begin{aligned} \vec{\mu}_{\text{expected}} &= \mathbf{H}_k \color{deeppink}{\mathbf{\hat{x}}_k} \\ \mathbf{\Sigma}_{\text{expected}} &= \mathbf{H}_k \color{deeppink}{\mathbf{P}_k} \mathbf{H}_k^T \end{aligned} \end{equation}\)

卡尔曼滤波的一大优点是擅长处理传感器噪声。换句话说，由于种种因素，传感器记录的信息其实是不准的，一个状态事实上可以产生多种读数。

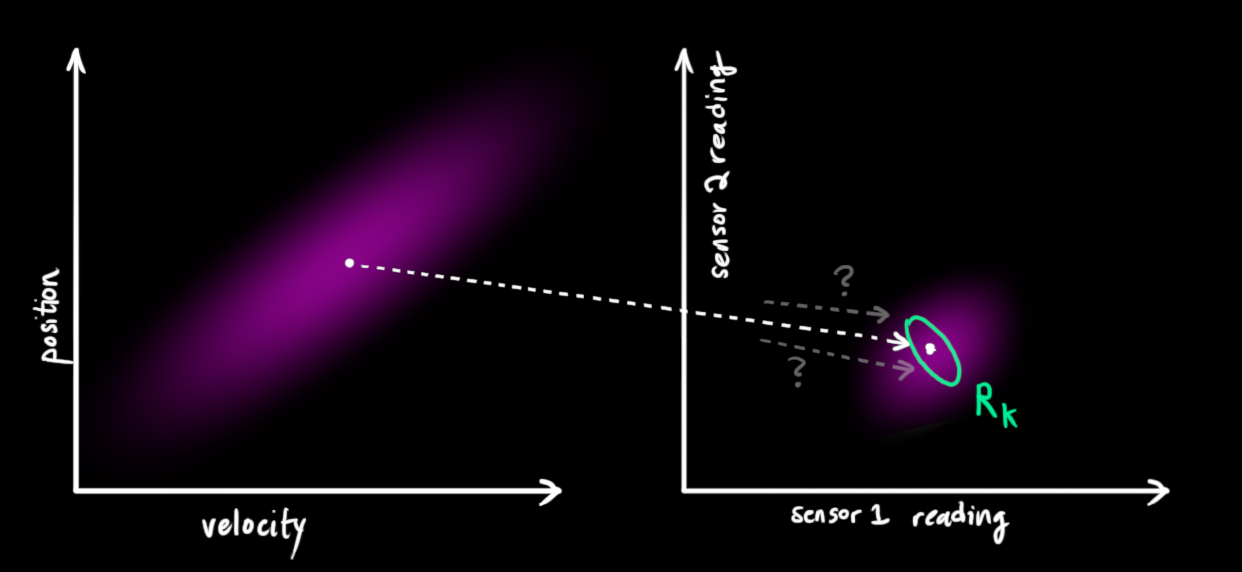
从我们观察到的每个读数中，我们可能会猜测我们的系统处于特定状态。但由于存在不确定性，一些状态比其他状态更有可能产生我们看到的读数：

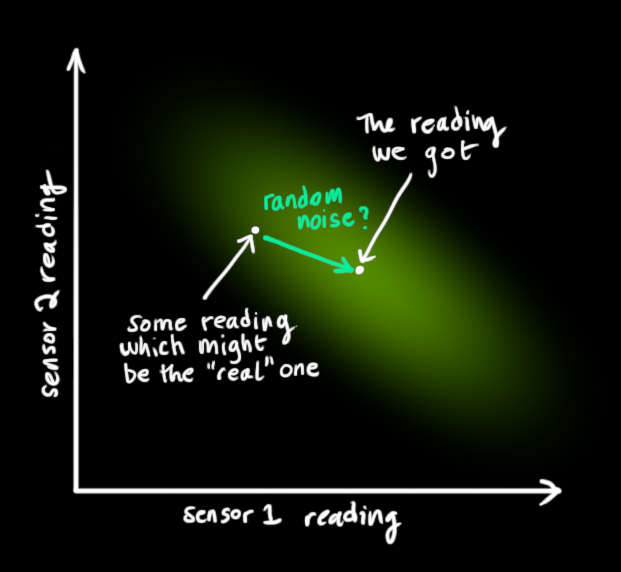
我们将这种不确定性（即传感器噪声）的协方差设为\(R_k\)，读数的分布均值设为\(z_k\)。

现在我们得到了两块高斯分布，一块围绕预测的均值，另一块围绕传感器读数。

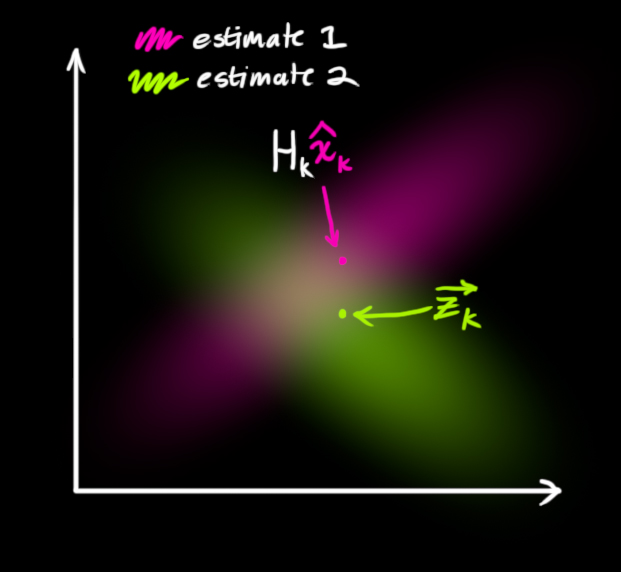
如果要生成靠谱预测，模型必须调和这两个信息。也就是说，对于任何可能的读数(z1,z2)，这两种方法预测的状态都有可能是准的，也都有可能是不准的。重点是我们怎么找到这两个准确率。

最简单的方法是两者相乘：

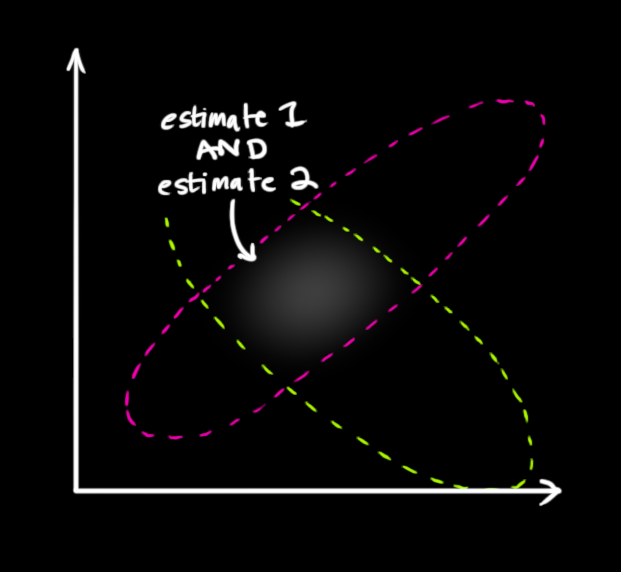
两块高斯分布相乘后，我们可以得到它们的重叠部分，这也是会出现最佳估计的区域。换个角度看，它看起来也符合高斯分布：

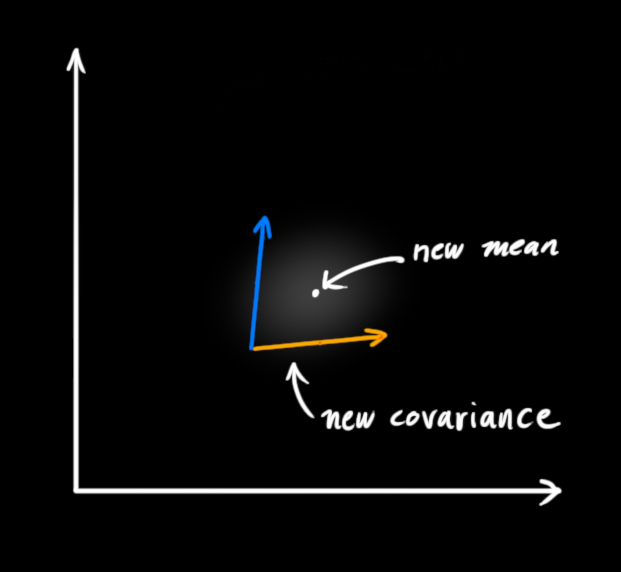
事实证明，当你把两个高斯分布和它们各自的均值和协方差矩阵相乘时，你会得到一个拥有独立均值和协方差矩阵的新高斯分布。最后剩下的问题就不难解决了：我们必须有一个公式来从旧的参数中获取这些新参数！

结合高斯

让我们从一维看起，设方差为\(\sigma^2\)，均值为 \(\mu\)，它是随机分布的中心；有一个方差一个标准一维高斯钟形曲线方程如下所示： \(\begin{equation} \label{gaussformula} \mathcal{N}(x, \mu,\sigma) = \frac{1}{ \sigma \sqrt{ 2\pi } } e^{ -\frac{ (x – \mu)^2 }{ 2\sigma^2 } } \end{equation}\)

那么两条高斯曲线相乘呢？

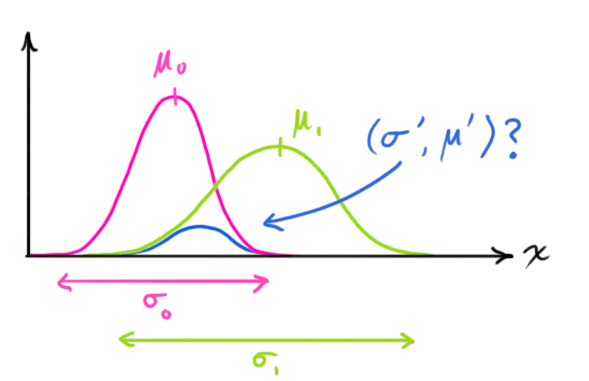
把这个式子按照一维方程进行扩展，可得：

如果有些太复杂，我们用k简化一下：

矩阵版本：

矩阵 \(K\) 就是我们说的卡尔曼增益

结合

截至目前，我们有用矩阵\((\color{fuchsia}{\mu_0}, \color{deeppink}{\Sigma_0}) = (\color{fuchsia}{\mathbf{H}_k \mathbf{\hat{x}}_k}, \color{deeppink}{\mathbf{H}_k \mathbf{P}_k \mathbf{H}_k^T})\)

预测的分布，有用传感器读数\((\color{yellowgreen}{\mu_1}, \color{mediumaquamarine}{\Sigma_1}) = (\color{yellowgreen}{\vec{\mathbf{z}_k}}, \color{mediumaquamarine}{\mathbf{R}_k})\)预测的分布。把它们代入上节的矩阵等式中：

卡尔曼增益就是：

化简后得：

最后， \(\color{royalblue}{\mathbf{\hat{x}}_k'}\)是我们的最佳估计值，我们可以把它继续放进去做另一轮预测：

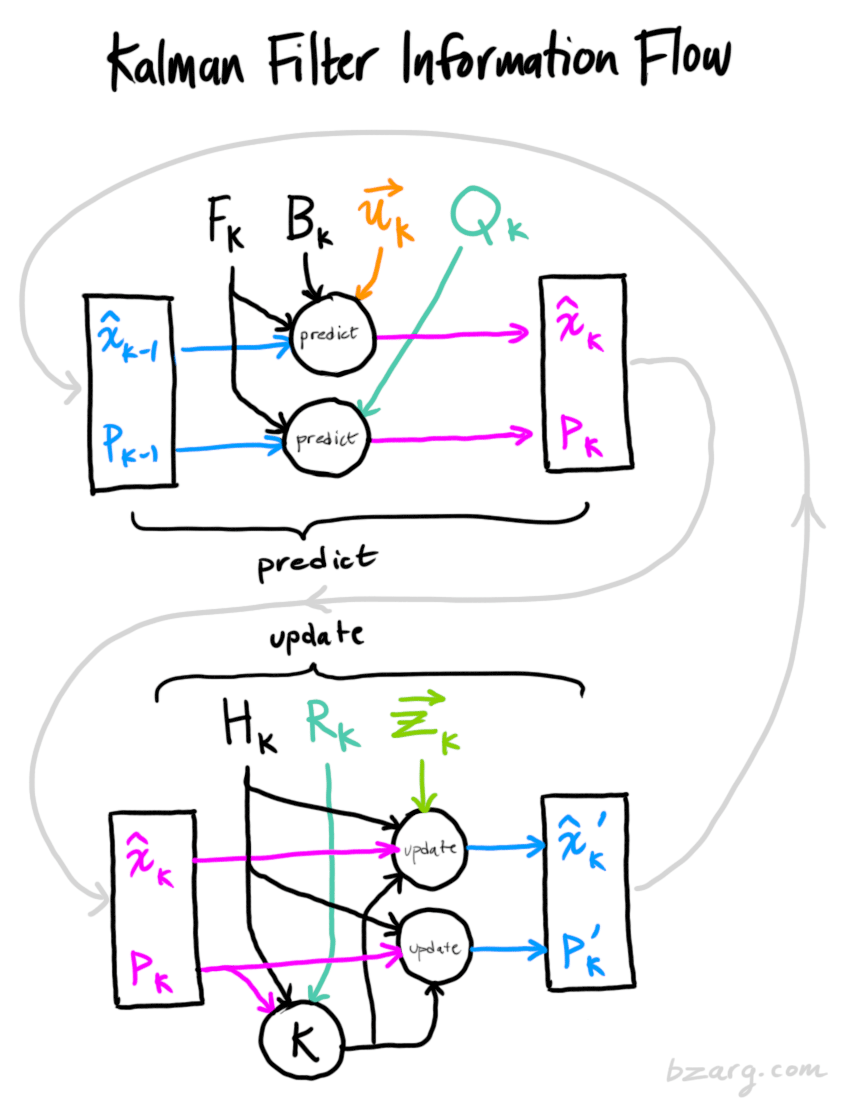
卡尔曼滤波将允许您准确地建模任何线性系统。对于非线性系统，我们使用扩展卡尔曼滤波器，它通过简单地线性化关于它们的平均值的预测和测量来工作。

总结

将上面的理论进行总结，可以得到下面几个公式，即卡尔曼滤波器的理性描述，使用下面的公式，就能够实现一个完整的卡尔曼滤波器

预测：

预测状态：\(\begin{equation} \begin{split} \color{deeppink}{\mathbf{\hat{x}}_k} &= \mathbf{F}_k \color{royalblue}{\mathbf{\hat{x}}_{k-1}} + \mathbf{B}_k \color{darkorange}{\vec{\mathbf{u}_k}} \\ \color{deeppink}{\mathbf{P}_k} &= \mathbf{F_k} \color{royalblue}{\mathbf{P}_{k-1}} \mathbf{F}_k^T + \color{mediumaquamarine}{\mathbf{Q}_k} \end{split} \end{equation}\)

更新：

卡尔曼增益： \(\begin{equation} \color{purple}{\mathbf{K}'} = \color{deeppink}{\mathbf{P}_k \mathbf{H}_k^T} ( \color{deeppink}{\mathbf{H}_k \mathbf{P}_k \mathbf{H}_k^T} + \color{mediumaquamarine}{\mathbf{R}_k})^{-1} \end{equation}\)

最佳估计：\(\begin{equation} \begin{split} \color{royalblue}{\mathbf{\hat{x}}_k'} &= \color{fuchsia}{\mathbf{\hat{x}}_k} & + & \color{purple}{\mathbf{K}'} ( \color{yellowgreen}{\vec{\mathbf{z}_k}} – \color{fuchsia}{\mathbf{H}_k \mathbf{\hat{x}}_k} ) \\ \color{royalblue}{\mathbf{P}_k'} &= \color{deeppink}{\mathbf{P}_k} & – & \color{purple}{\mathbf{K}'} \color{deeppink}{\mathbf{H}_k \mathbf{P}_k} \end{split} \end{equation}\)

参数解释：

\(\hat{x}_k\):状态向量。

\(F_k\):状态转移矩阵,为常数。

\(B_k\):控制矩阵。受外部环境影响，可为空。

\(\vec{\mathbf{u}_k}\):控制向量。受外部环境影响，可为空。

\(P_k\):协方差矩阵,为常数。

\(Q_k\):预测噪声协方差矩阵，为常数。

\(R_k\):观测噪声协方差矩阵,为常数。

\(\mathbf{K}'\):计算出的卡尔曼增益。

\(H_k\):观测矩阵。为常数。

\(\mathbf{z}_k\):测量值向量。

代码

KF.h

#ifndef KF_H
#define KF_H

#include "../lib/Eigen/Dense"


class KalmanFilter
{
private:
    int stateSize; //state variable's dimenssion
    int measSize; //measurement variable's dimession
    int uSize; //control variables's dimenssion
    Eigen::VectorXd x; //状态
    Eigen::VectorXd z; //测量值

    Eigen::MatrixXd A; //状态转移矩阵
    Eigen::MatrixXd B; //输入控制矩阵

    Eigen::VectorXd u; //控制向量，外界对系统的作用

    Eigen::MatrixXd P; //coveriance
    Eigen::MatrixXd H; //观测矩阵
    Eigen::MatrixXd R; //measurement noise covariance
    Eigen::MatrixXd Q; //process noise covariance

    void CalculateJacobianMatrix();

public:
    KalmanFilter(int stateSize_=0, int measSize_=0,int uSize_=0);//构造函数
    ~KalmanFilter(){} //析构函数
    void init(Eigen::VectorXd &x_, Eigen::MatrixXd& P_,Eigen::MatrixXd& R_, Eigen::MatrixXd& Q_);
    Eigen::VectorXd predict(Eigen::MatrixXd& A_);
    Eigen::VectorXd predict(Eigen::MatrixXd& A_, Eigen::MatrixXd &B_, Eigen::VectorXd &u_);
    void KFUpdate(Eigen::MatrixXd& H_, Eigen::VectorXd z_meas);
    void EKFUpdate(Eigen::MatrixXd& H_, Eigen::VectorXd z_meas);
};

#endif //KF_H

KF.cpp

#include <iostream>
#include "KF.h"
using namespace std;

KalmanFilter::KalmanFilter(int stateSize_, int measSize_, int uSize_) :stateSize(stateSize_), measSize(measSize_), uSize(uSize_)
{
    if (stateSize == 0 || measSize == 0)
    {
        std::cerr << "Error, State size and measurement size must bigger than 0\n";
    }

    x.resize(stateSize);
    x.setZero();

    A.resize(stateSize, stateSize);
    A.setIdentity();

    u.resize(uSize);
    u.transpose();
    u.setZero();

    B.resize(stateSize, uSize);
    B.setZero();

    P.resize(stateSize, stateSize);
    P.setIdentity();

    H.resize(measSize, stateSize);
    H.setZero();

    z.resize(measSize);
    z.setZero();

    Q.resize(stateSize, stateSize);
    Q.setZero();

    R.resize(measSize, measSize);
    R.setZero();
}

void KalmanFilter::init(Eigen::VectorXd &x_, Eigen::MatrixXd& P_, Eigen::MatrixXd& R_, Eigen::MatrixXd& Q_)
{
    x = x_;
    P = P_;
    R = R_;
    Q = Q_;
}

// 已知控制矩阵B和控制向量u
Eigen::VectorXd KalmanFilter::predict(Eigen::MatrixXd& A_, Eigen::MatrixXd &B_, Eigen::VectorXd &u_)
{
    A = A_;
    B = B_;
    u = u_;
    x = A * x + B * u;
    Eigen::MatrixXd F_T = A.transpose();
    P = A * P * F_T + Q;
    return x;
}

// 未知控制矩阵B和控制向量u
Eigen::VectorXd KalmanFilter::predict(Eigen::MatrixXd& A_)
{
    A = A_;
    x = A * x;
    Eigen::MatrixXd A_T = A.transpose();
    P = A * P * A_T + Q;
//    cout << "P-=" << P<< endl;
    return x;
}

void KalmanFilter::KFUpdate(Eigen::MatrixXd& H_, Eigen::VectorXd z_meas)
{
    H = H_;
    Eigen::MatrixXd S,Ht;
    Ht = H.transpose();
    S = H * P * Ht + R;
    Eigen::MatrixXd K = P*Ht*S.inverse(); //卡尔曼增益
    z = H * x;
    x = x + K * (z_meas - z);
    Eigen::MatrixXd I = Eigen::MatrixXd::Identity(stateSize, stateSize);
    P = (I - K * H) * P;
//    cout << "P=" << P << endl;
}

参考链接

• https://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/
• https://zhuanlan.zhihu.com/p/45238681