1.NLP介绍与词向量初步
第1课直接切入语言和词向量,讲解了自然语言处理的基本概念,文本表征的方法和演进,包括word2vec等核心方法,词向量的应用等。
1.自然语言与词汇含义
1.1 人类的语言与词汇含义
人类之所以比类人猿更"聪明",是因为我们有语言,因此是一个人机网络,其中人类语言作为网络语言。人类语言具有信息功能和社会功能。
据估计,人类语言只有大约5000年的短暂历史。语言和写作是让人类变得强大的原因之一。它使知识能够在空间上传送到世界各地,并在时间上传送。
但是,相较于如今的互联网的传播速度而言,人类语言是一种缓慢的语言。然而,只需人类语言形式的几百位信息,就可以构建整个视觉场景。这就是自然语言如此迷人的原因。
1.2 我们如何表达一个词的意思?
我们如何表达一个词的含义呢?有如下一些方式:
- 用一个词、词组等表示的概念
- 一个人想用语言、符号等来表达的想法
- 表达在作品、艺术等方面的思想
理解意义的最普遍的语言方式(linguistic way):语言符号与语言意义(想法、事情)的相互对应
denotational semantics:语义
signifier(symbol) <=> signifier(idea or thing)
1.3 如何在计算机里表达词的意义
要使用计算机处理文本词汇,一种处理方式是WordNet:即构建一个包含同义词集和上位词("is a"关系)的列表的辞典。英文当中确实有这样一个 wordnet,我们在安装完NLTK工具库和下载数据包后可以使用,对应的 python 代码如下:
from nltk.corpus import wordnet as wn
poses = { 'n':'noun', 'v':'verb', 's':'adj (s)', 'a':'adj', 'r':'adv'}
for synset in wn.synsets("good"):
print("{}: {}".format(poses[synset.pos()], ", ".join([l.name() for l in synset.lemmas()])))
from nltk.corpus import wordnet as wn
panda = wn.synset("panda.n.01")
hyper = lambda s: s.hypernyms()
list(panda.closure(hyper))
noun: good
noun: good, goodness
noun: good, goodness
noun: commodity, trade_good, good
adj: good
adj (s): full, good
adj: good
adj (s): estimable, good, honorable, respectable
adj (s): beneficial, good
adj (s): good
adj (s): good, just, upright
adj (s): adept, expert, good, practiced, proficient, skillful, skilful
adj (s): good
adj (s): dear, good, near
adj (s): dependable, good, safe, secure
adj (s): good, right, ripe
adj (s): good, well
adj (s): effective, good, in_effect, in_force
adj (s): good
adj (s): good, serious
adj (s): good, sound
adj (s): good, salutary
adj (s): good, honest
adj (s): good, undecomposed, unspoiled, unspoilt
adj (s): good
adv: well, good
adv: thoroughly, soundly, good
[Synset('procyonid.n.01'),
Synset('carnivore.n.01'),
Synset('placental.n.01'),
Synset('mammal.n.01'),
Synset('vertebrate.n.01'),
Synset('chordate.n.01'),
Synset('animal.n.01'),
Synset('organism.n.01'),
Synset('living_thing.n.01'),
Synset('whole.n.02'),
Synset('object.n.01'),
Synset('physical_entity.n.01'),
Synset('entity.n.01')]
1.4 WordNet的问题
大家可以将WordNet视作1个专家经验总结出来的词汇表,但它存在一些问题:
- 忽略了词汇的细微差别
- 例如"proficient"被列为"good"的同义词。这只在某些上下文中是正确的。
- 缺少单词的新含义
- 难以持续更新!
- 例如:wicked、badass、nifty、wizard、genius、ninja、bombast
- 因为是小部分专家构建的,有一定的主观性
- 构建与调整都需要很多的人力成本
- 无法定量计算出单词相似度
1.5 文本(词汇)的离散表征
在传统的自然语言处理中,我们会对文本做离散表征,把词语看作离散的符号:例如hotel、conference、motel等。
一种文本的离散表示形式是把单词表征为独热向量(one-hot vectors)的形式
独热向量:只有一个1,其余均为0的稀疏向量
在独热向量表示中,向量维度 = 词汇量(如500,000),以下为一些独热向量编码过后的单词向量示例:
motel = [0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]
hotel = [0 0 0 0 0 0 0 1 0 0 0 0 0 0 0]
1.6 离散表征的问题
在上述的独热向量离散表征里,所有词向量是正交的,这是一个很大的问题。对于独热向量,没有关于相似性概念,并且向量维度过大。
对于上述问题有一些解决思路:
- 使用类似WordNet的工具中的列表,获得相似度,但会因不够完整而失败
- 通过大量数据学习词向量本身相似性,获得更精确的稠密词向量编码
1.7 基于上下文的词汇表征
近年来在深度学习中比较有效的方式是基于上下文的词汇表征。它的核心想法是:一个单词的意思是由经常出现在它附近的单词给出的 "You shall know a word by the company it keeps" (J. R. Firth 1957: 11)。
- 这是现代统计NLP最成功的理念之一
- 总体思路有点物以类聚,人以群分的感觉。
当一个单词\(w\)出现在文本中时,它的上下文是出现在其附近的一组单词(在一个固定大小的窗口中) 基于海量数据,使用\(w\)的许多上下文来构建\(w\)的表示
如图所示,banking的含义可以根据上下文的内容表征。

2.Word2vec介绍
2.1 词向量表示
下面我们要介绍词向量的构建方法与思想,我们希望为每个单词构建一个稠密表示的向量,使其与出现在相似上下文中的单词向量相似。

词向量(word vectors)有时被称为词嵌入(word embeddings)或词表示(word representations)。
稠密词向量是分布式表示(distributed representation)。
2.2 Word2vec原理介绍
Word2vec (Mikolov et al. 2013)是一个学习词向量表征的框架。
核心思路如下:
- 基于海量文本语料库构建
- 词汇表中的每个单词都由一个向量表示(学习完成后会固定)
- 对应语料库文本中的每个位置\(t\),有一个中心词\(c\)和一些上下文("外部")单词\(o\)
- 使用\(c\)和\(o\)的词向量来计算概率\(P(o \mid c)\),即给定中心词推断上下文词汇的概率(反之亦然)
- 不断调整词向量来最大化这个概率
下图为窗口大小j=2时的\(P(w_{t+j}\mid w_t)\)它的中心词为into
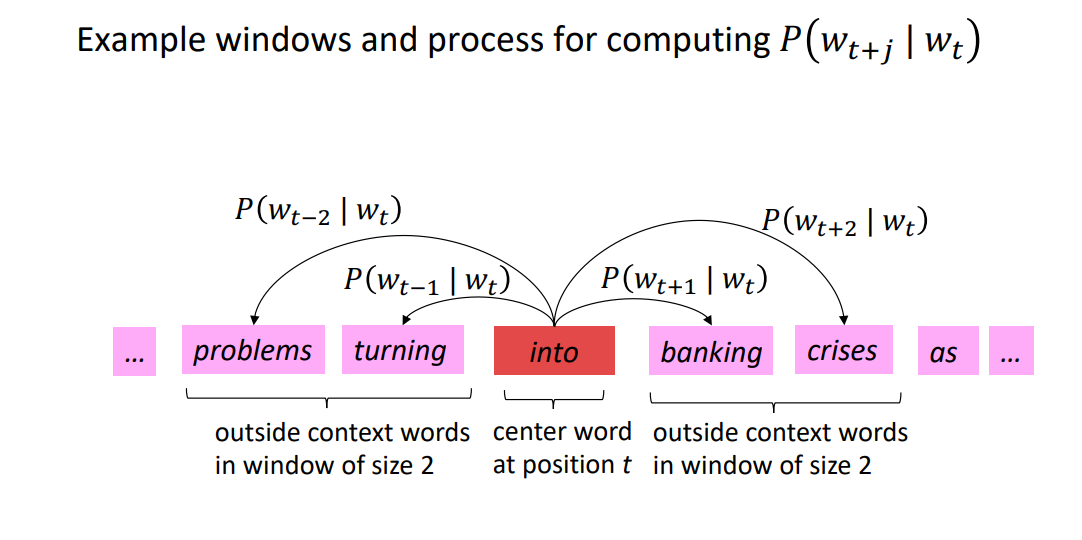
下图为窗口大小j=2时的\(P(w_{t+j} \mid w_t)\)它的中心词为banking
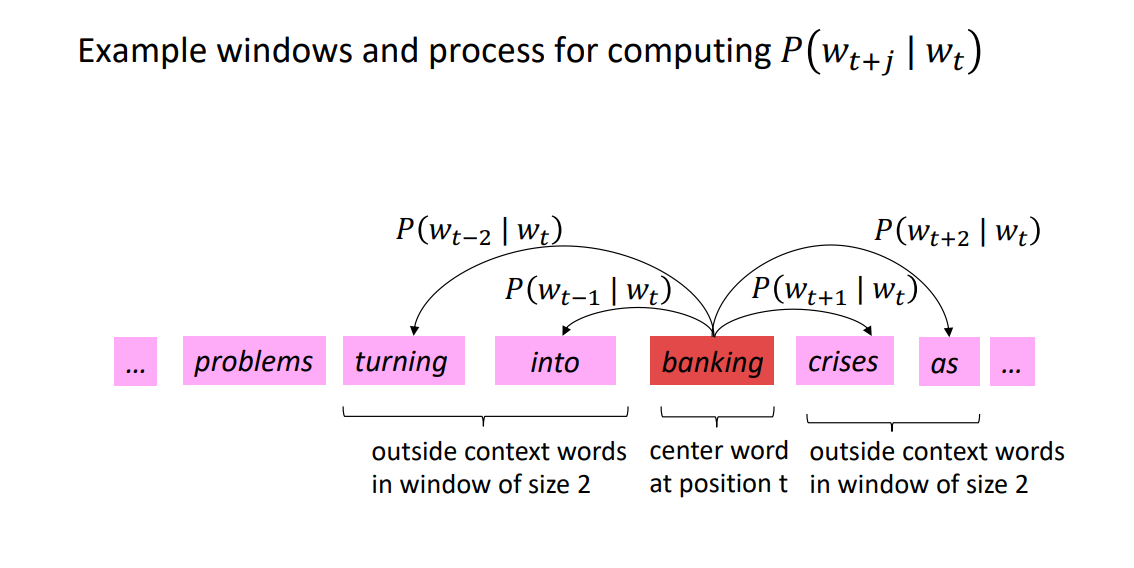
3.Word2vec目标函数
3.1 Word2vec目标函数
3.1.1 似然函数
对于每个位置\(t=1,...,T\),在大小为\(m\)的固定窗口内预测上下文单词,给定中心词\(w_j\),似然函数可以表示为:
\[\text { Likelihoood }=L(\theta)=\prod_{t=1}^{T} \prod_{\substack{m \leq j \leq m \\ j \neq 0}} P\left(w_{t+j} \mid w_{t} ; \theta\right)\]上述公式中,\(\theta\) 为模型包含的所有待优化权重变量.
3.1.2 目标函数
对应上述似然函数的目标函数 \(J(\theta)\) 可以取作(平均)负对数似然:
\[J(\theta)=-\frac{1}{T} \log L(\theta)=-\frac{1}{T} \sum_{t=1}^{T} \sum_{\substack{-m \leq j \leq m \\ j \neq 0}} \log P\left(w_{t+j} \mid w_{t} ; \theta\right)\]注意: 目标函数 \(J(\theta)\) 有时也被称为"代价函数"或"损失函数"
最小化目标函数 <=> 最大化似然函数(预测概率/精度),两者等价
补充:
- 上述目标函数中的log形式是方便将连乘转化为求和,负号是希望将极大化似然率转化为极小化损失函数的等价问题
- 在连乘之前使用log转化为求和非常有效,特别是做优化时 \(\log \prod_{i} x_{i}=\sum_{i} \log x_{i}\) 得到目标函数后,我们希望最小化目标函数,那我们如何计算 \(P\left(w_{t+j} \mid w_{t} ; \theta\right)\)
对于每个词 \(w\) 都会用两个向量:
当 \(w\) 是中心词时,我们标记词向量为 \(v_w\) 当 \(w\) 是上下文词时,我们标记词向量为 \(u_w\)
则对于一个中心词 \(c\) 和一个上下文词 \(o\),我们有如下概率计算方式: \(P(o \mid c)=\frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)}\)
- 公式中,向量 \(u_o\) 和向量 \(v_c\) 进行点乘
- 向量之间越相似,点乘结果越大,从而归一化后得到的概率值也越大
- 模型的训练正是为了使得具有相似上下文的单词,具有相似的向量
- 点积是计算相似性的一种简单方法,在注意力机制中常使用点积计算 Score
3.2 从向量视角回顾Word2vec
下图为计算 \(P\left(w_{t+j} \mid w_{t}\right)\) 的示例,这里把 \(P\left(\text { problems } \mid \text { into } ; u_{\text {problems }}, v_{\text {into }}, \theta\right)\) 简写为 \(P\left(u_{\text {problems }} \mid v_{\text {into }}\right)\),例子中的上下文窗口大小2,即"左右2个单词+一个中心词"。
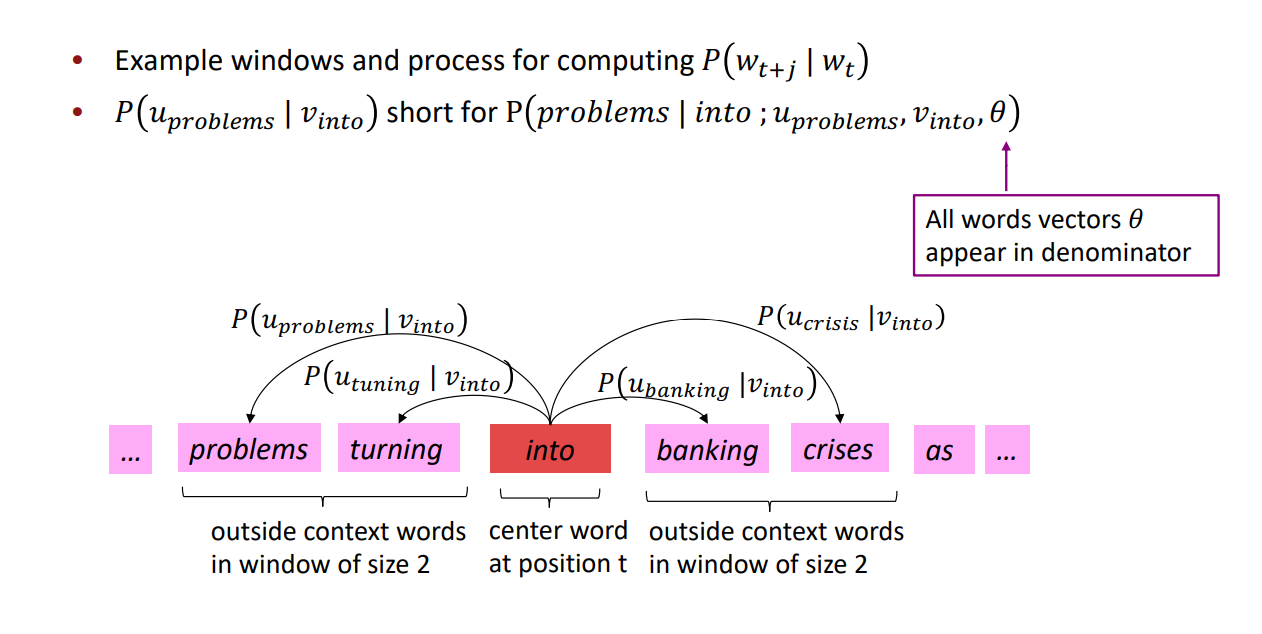
4.Word2vec预测函数
4.1 Word2vec预测函数
回到上面的概率计算,我们来观察一下 \(P(o \mid c)=\frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)}\)
- 取幂使任何数都为正
- 点积比较 \(o\) 和 \(c\) 的相似性 \(u^{T} v=u . v=\sum_{i=1}^{n} u_{i} v_{i}\),点积越大则概率越大
- 分母:对整个词汇表进行标准化,从而给出概率分布
这里有一个softmax的概率,softmax function 将任意值 \(x_i\) 映射到概率分布 \(p_i\)
\[\operatorname{softmax}\left(x_{i}\right)=\frac{\exp \left(x_{i}\right)}{\sum_{j=1}^{n} \exp \left(x_{j}\right)}=p_{i}\]其中对于名称中soft和max的解释如下(softmax在深度学习中经常使用到):
- max:因为放大了最大的概率
- soft:因为仍然为较小的 \(x_i\) 赋予了一定概率
4.2 word2vec中的梯度下降训练细节推导
下面是对于word2vec的参数更新迭代,应用梯度下降法的一些推导细节
首先我们随机初始化 \(u_{w} \in \mathbb{R}^{d}\) 和 \(v_{w} \in \mathbb{R}^{d}\),而后使用梯度下降法进行更新
\[\begin{aligned} \frac{\partial}{\partial v_{c}} \log P(o \mid c) &=\frac{\partial}{\partial v_{c}} \log \frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} \\ &=\frac{\partial}{\partial v_{c}}\left(\log \exp \left(u_{o}^{T} v_{c}\right)-\log \sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)\right) \\ &=\frac{\partial}{\partial v_{c}}\left(u_{o}^{T} v_{c}-\log \sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)\right) \\ &=u_{o}-\frac{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right) u_{w}}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} \end{aligned}\]偏导数可以移进求和中,对应上方公式的最后两行的推导
\[\frac{\partial}{\partial x} \sum_{i} y_{i}=\sum_{i} \frac{\partial}{\partial x} y_{i}\]对上述结果重新排列如下,第一项是真正的上下文单词,第二项是预测的上下文单词。使用梯度下降法,模型的预测上下文将逐步接近真正的上下文。
\[\begin{aligned} \frac{\partial}{\partial v_{c}} \log P(o \mid c) &=u_{o}-\frac{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right) u_{w}}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} \\ &=u_{o}-\sum_{w \in V} \frac{\exp \left(u_{w}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} u_{w} \\ &=u_{o}-\sum_{w \in V} P(w \mid c) u_{w} \end{aligned}\]再对 \(u_o\) 进行偏微分计算,注意这里的 \(u_o\) 是 \(u_{w=o}\) 的简写,故可知
\[\begin{aligned} \frac{\partial}{\partial u_{o}} \sum_{w \in V} u_{w}^{T} v_{c} &=\frac{\partial}{\partial u_{o}} u_{o}^{T} v_{c}=\frac{\partial u_{o}}{\partial u_{o}} v_{c}+\frac{\partial v_{c}}{\partial u_{o}} u_{o}=v_{c} \\ \frac{\partial}{\partial u_{o}} \log P(o \mid c) &=\frac{\partial}{\partial u_{o}} \log \frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} \\ &=\frac{\partial}{\partial u_{o}}\left(\log \exp \left(u_{o}^{T} v_{c}\right)-\log \sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)\right) \\ &=\frac{\partial}{\partial u_{o}}\left(u_{o}^{T} v_{c}-\log \sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)\right) \\ &=v_{c}-\frac{\sum_{\frac{\partial}{\partial u_{o}}} \exp \left(u_{w}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} \\ &=v_{c}-\frac{\exp \left(u_{o}^{T} v_{c}\right) v_{c}}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} \\ &=v_{c}-\frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} v_{c} \\ &=v_{c}-P(o \mid c) v_{c} \\ &=(1-P(o \mid c)) v_{c} \end{aligned}\]可以理解,当 \(P(o \mid c) \rightarrow 1\),即通过中心词 \(c\) 我们可以正确预测上下文词 \(o\),此时我们不需要调整 \(u_o\),反之,则相应调整 \(u_o\)。
训练模型的过程,实际上是我们在调整参数最小化损失函数。
如下是一个包含2个参数的凸函数,我们绘制了目标函数的等高线。
\(\theta\) 代表所有模型参数,写在一个长的参数向量里。
在我们的场景汇总是 \(d\) 维向量空间的 \(V\) 个词汇。
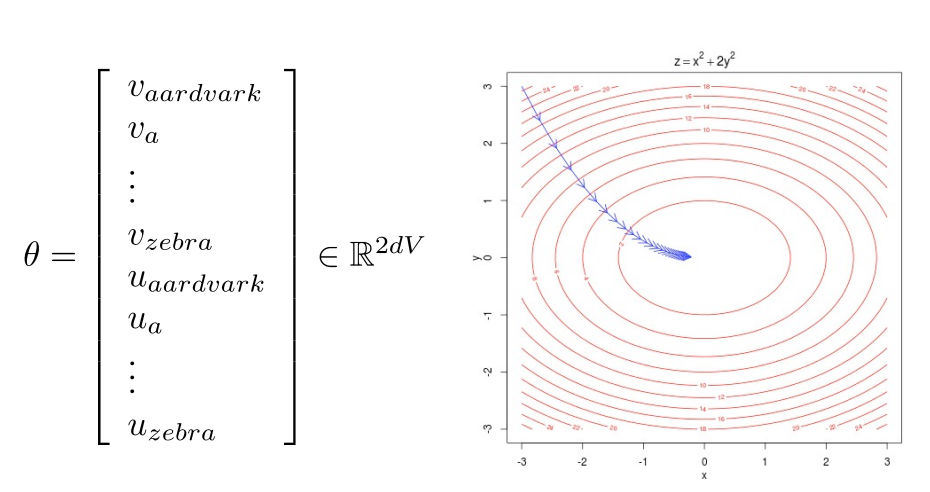
5.优化函数
5.1 Gradient Descent
Gradient Descent是一种可以最小化\(J(\theta)\)的算法。
思想: 对于\(\theta\),计算\(J(\theta)\),朝负梯度方向迈出一小步,重复上述步骤。
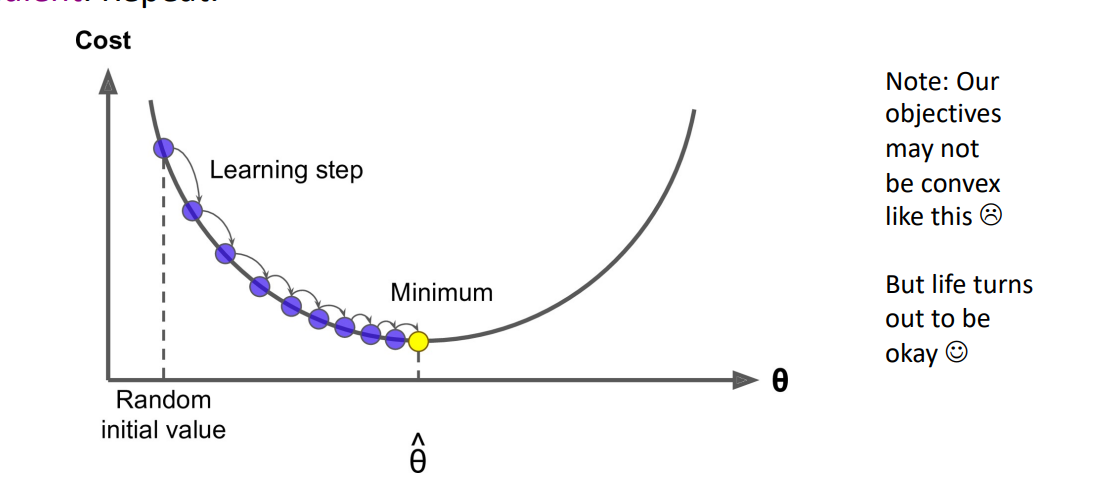
更新公式(用矩阵表示法):
\[\theta^{n e w}=\theta^{\text {old }}-\alpha \nabla_{\theta} J(\theta)\]更新公式(对于单一参数):
\[\theta_{j}^{\text {new }}=\theta_{j}^{\text {old }}-\alpha \frac{\partial}{\partial \theta_{j}^{\text {old }}} J(\theta)\]算法:
while true:
theta_grad = evaluate_gradient(J, corpus, theta)
theta = theta - alpha * theta_grad
Stochastic Gradient Descent
问题:\(J(\theta)\) 在corpus中是一种全窗口的函数,所以\(\nabla_{\theta} J(\theta)\)有昂贵的计算代价。
解决方法: Stochastic Gradient Descent(SGD)
- 重复采样窗口,迭代更新
算法:
while true:
window = sample_window(corpus)
theta_grad = evaluate_gradient(J, window, theta)
theta = theta - alpha * theta_grad