006

英文名称： GloVe: Global Vectors for Word Representation

中文名称： 基于全局共现信息的词表示

论文地址： https://aclanthology.org/D14-1162.pdf

期刊/时间： EMNLP 2014

前置知识

One-hot编码

One-hot编码，又称独热编码，其方法是使用N位状态寄存器来对N个状态进行编码，每个状态都有它独立的寄存器位，并且在任意时候，其中只有一位有效。One-hot在特征提取上属于词袋模型（bag of words）。

词袋模型未考虑次序，假设词与词相互独立，高维、离散、稀疏

词表示发展历史

趋势：让词的语义更准确地编码到有限维的向量中，在向量子空间中保持词的语义关系。

基于独热的词表示
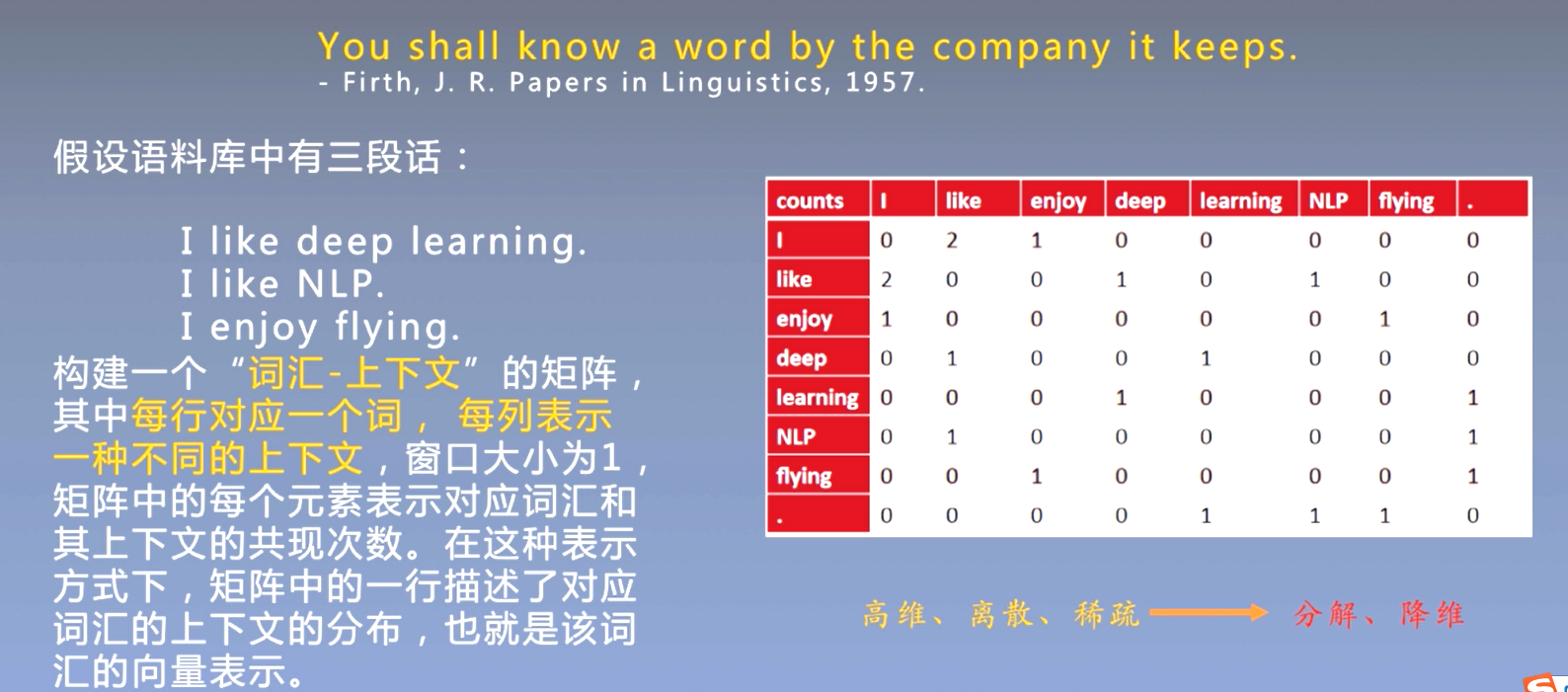
基于共现矩阵的词表示
- 基于矩阵奇异值分解的词表示
  - 基本思想：利用奇异值分解（SVD）方法对贡献矩阵进行分解。这种方法可以看作是对频率矩阵进行降噪和降维处理，并从中挖掘出词汇的潜在含义。类似方法还有NMF、CCA等
  - SVD得到了word的稠密矩阵，该矩阵具有很多良好的性质：语义相近的词在向量空间相近，甚至可以一定程度反映word间的线性关系。但也具有一些缺点：
    - 矩阵维度经常变动, 比如新词频繁加入
    - 绝大部分词不会共现, 矩阵过于稀疏
    - 矩阵维度很高, 大约是 $10^6 \times 10^6$
    - 训练时的计算复杂度是 $O\left( V ^3\right)$
基于神经网络的词表示
- CBOW
- Skip-gram

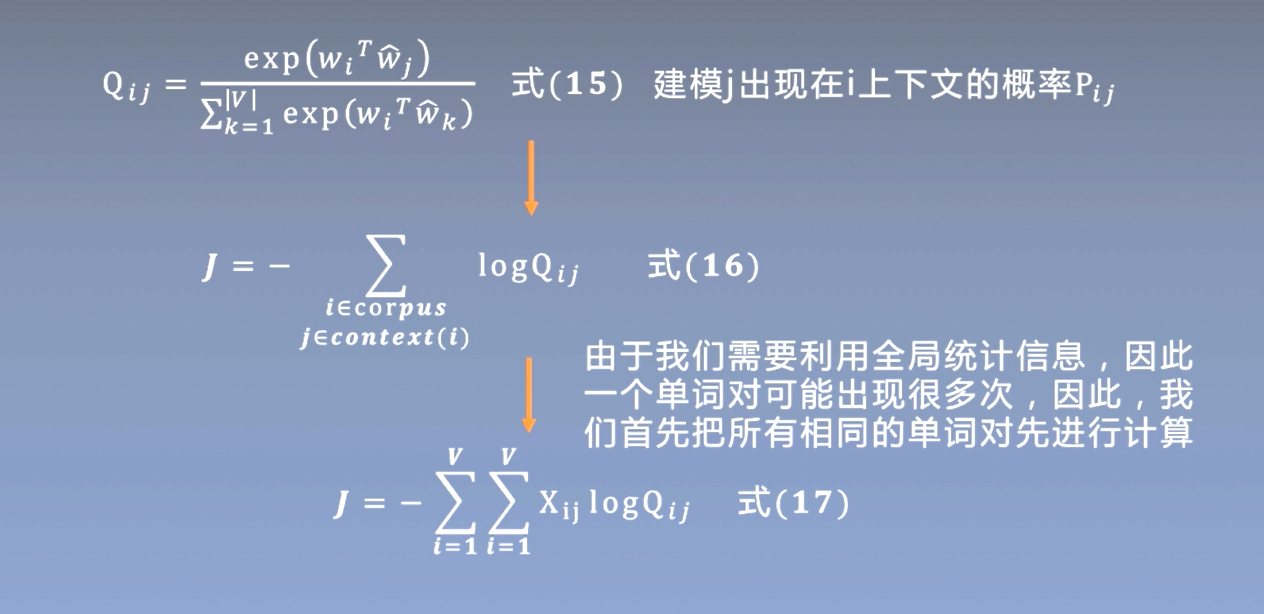
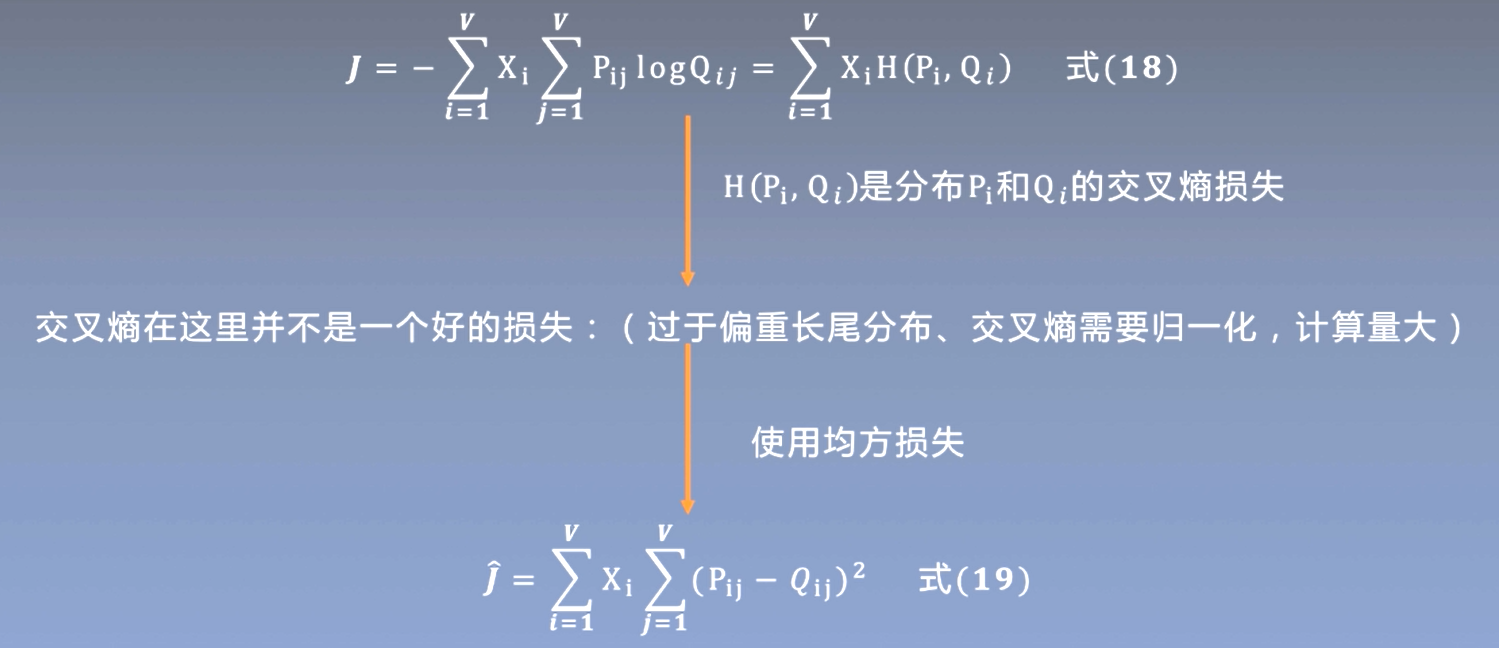
基于矩阵分解的词表示方法：首先统计语料库中的 "词-文档" 或者 "词-词" 共现矩阵，然后通过矩阵分解的方法来获得一个低维词向量。

优点 : 利用全局统计信息
缺点：时间复杂度高、过度重视共现词频高的单词对 基于神经网络的词表示方法：通过神经网络使上下文窗口内频繁共现的单词对的表示接近
优点：效果较好、速度快
缺点：没有充分利用全局统计信息、过度重视共现词频高的单词对

GloVe：取长补短，结合两种方法的优点学习词表示

摘要

问题是什么？
- 语义与语法的规律是晦涩难懂的
我们要做什么？
- 通过分析了上述规律出现在词向量中所需的模型属性，提出了一种新的全局对数双线性回归模型，结合了全局矩阵分解与局部上下文窗口方法。
大概怎么做的
- 我们的模型通过仅在词-词共现矩阵中的非零元素上进行训练，而不是在整个稀疏矩阵或大型语料库中的单个上下文窗口上进行训练，从而有效地利用了统计信息。
实验效果
- 在最近的词类比任务中的表现达到了75%，同时在相似性任务和命名实体识别任务上表现SOTA。

介绍

按照起承转合的思想阅读。

起。做的哪方面工作？
- 语言的语义向量空间模型用实值向量表示每个单词。
承。相关工作
- 大多数词向量方法依赖于词向量对之间的距离或角度作为评估这样一组词表示的内在质量的主要方法。
- Mikolov提出了一种新的评估方法，该方法不是检查词向量之间的标量距离，而是检查他们之间不同维度的差异。
- For example, the analogy "king is to queen as man is to woman" should be encoded in the vector space by the vector equation king − queen = man − woman.
- 这种方法有利于产生有意义的模型，从而捕捉分布式表示的多聚类思想
转。相关工作的不足和转机
- 下面的两种方法都存在缺点。
  - 全局矩阵分解方法，例如潜在语义分析 (LSA)，虽然像 LSA 有效地利用了统计信息，但它们在词类比任务上的表现相对较差，这表明向量空间结构是次优的。
  - 局部上下文窗口方法，例如skip-gram 模型。像 skip-gram 这样的方法在类比任务上可能做得更好，但它们对语料库的统计数据的利用不佳，因为它们是在单独的局部上下文窗口而不是全局共现计数上训练的。
合。本文工作
- 在这项工作中，我们分析了产生线性意义方向所必需的模型属性，并认为全局对数双线性回归模型适合这样做。
- 我们提出了一个特定的加权最小二乘模型，该模型可以训练全局词词共现计数，从而有效地利用统计数据。
- 该模型生成具有有意义子结构的词向量空间，其在词类比数据集上的 75% 准确率的最新性能证明了这一点。我们还证明了我们的方法在几个单词相似性任务以及常见的命名实体识别（NER）基准上优于其他当前方法。

方法

简要地重复问题
- 语料库中单词出现的统计数据是所有用于学习单词表示的无监督方法的主要信息来源，尽管现在存在许多这样的方法，但问题仍然是如何从这些统计数据中产生意义，以及结果词向量如何表示这个意义。
解决思路
- 构建了一个新的单词表示模型，我们称之为 GloVe，用于全局向量，因为全局语料库统计数据直接由模型捕获。
必要的形式化定义
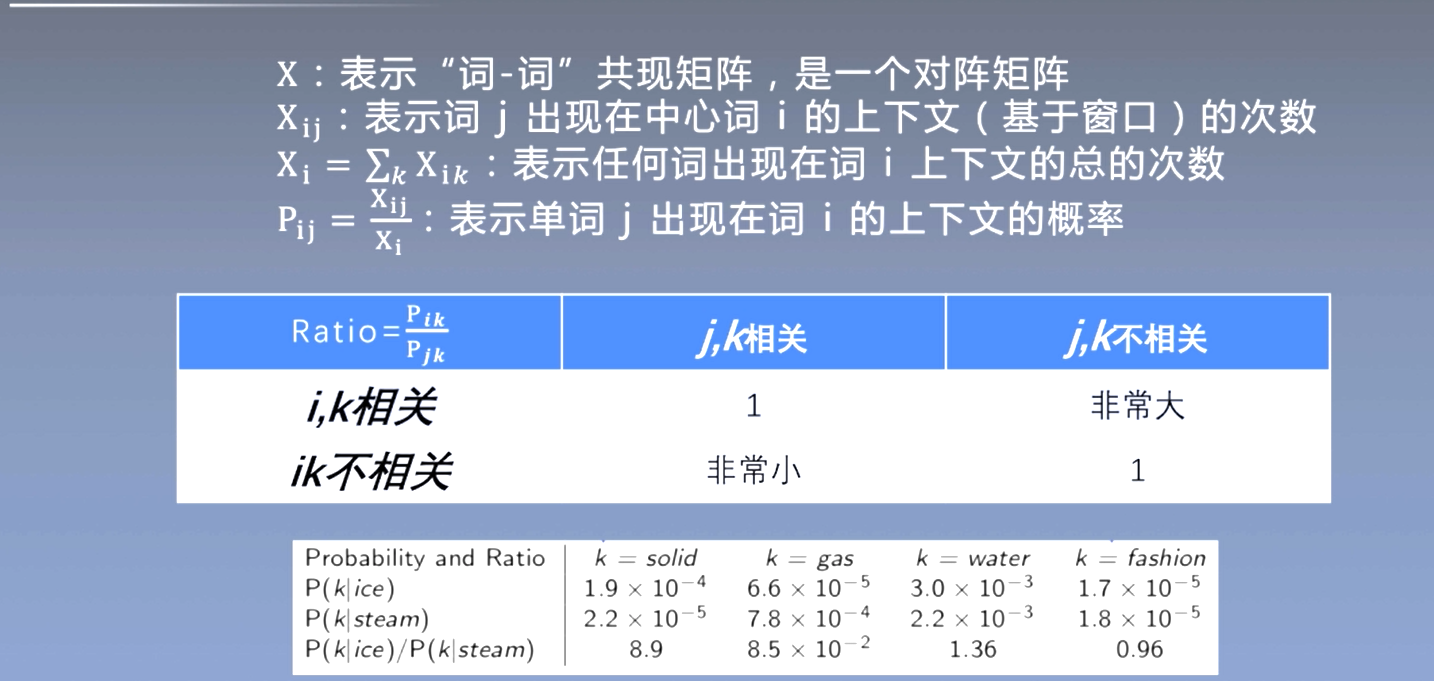
$X$ : 表示 "词-词" 共现矩阵，是一个对阵矩阵 $\mathrm{X}{\mathrm{ij}}$ ：表示词 $\mathrm{j}$ 出现在中心词 $\mathrm{i}$ 的上下文（基于窗口 ) 的次数 $\mathrm{X}{\mathrm{i}}=\sum_k \mathrm{X}{\mathrm{i} k}$ : 表示任何词出现在词 $\mathrm{i}$ 上下文的总的次数 $P{i j}=\frac{x_{i j}}{x_i}$ : 表示单词 $\mathrm{j}$ 出现在词 $\mathrm{i}$ 的上下文的概率
具体模型
- 通过实验统计证明，词向量学习的合适起点应该是共现概率的比率，而不是概率本身。
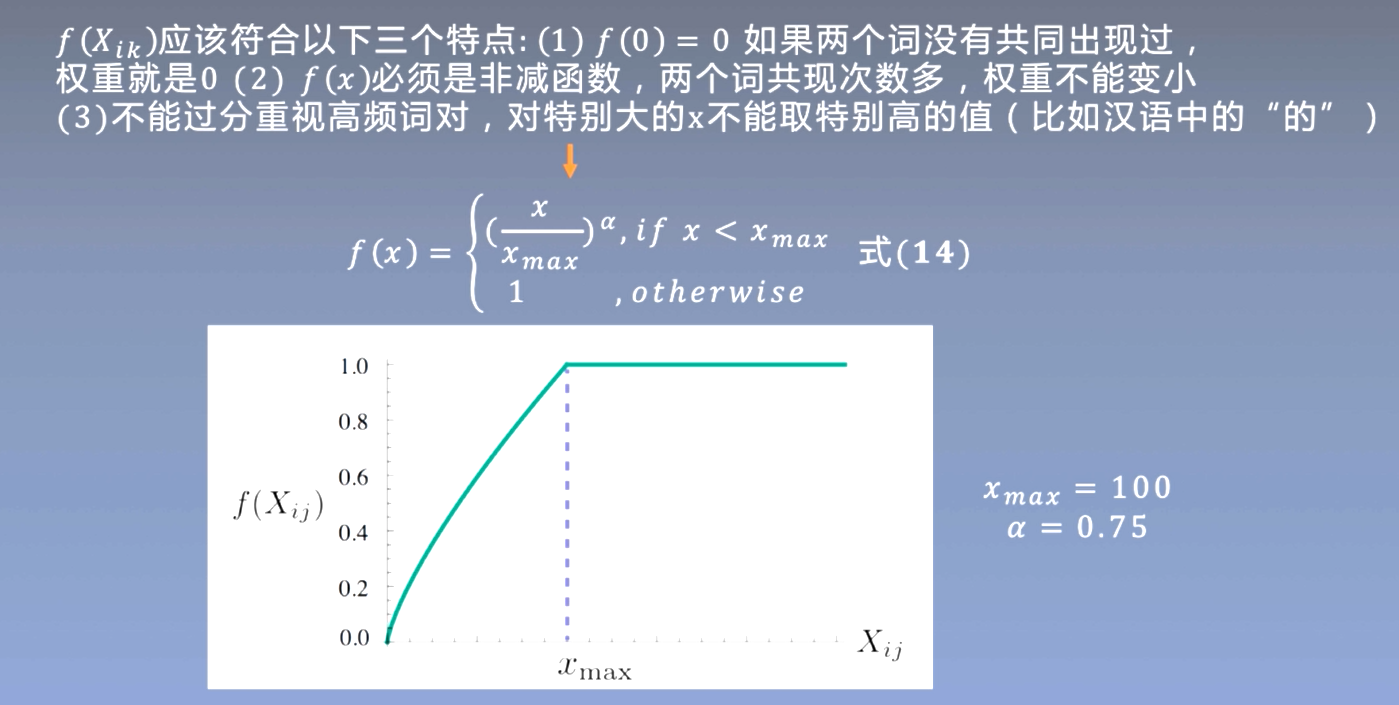
- 一个词具有两个向量（中心词和上下文词），采用相加的方式将两个向量融合为一个
  
  实验
数据集和实验设置
主实验，提供详尽的实验分析
- Word analogies: " $\mathrm{a}$ is to $\mathrm{b}$ as $\mathrm{c}$ is to ?" 遍历词典，找到和 $w_b-w_a+w_c$ 最接近 ( 余弦相似度最大) 的词
- Word similarity : 两个单词语义相似性计算（余弦相似度）
- NER：命名实体识别