005

英文名称： Attention Is All You Need

中文名称： Attention Is All You Need

论文地址： http://arxiv.org/abs/1706.03762

期刊/时间：NIPS 2017

前置知识

序列模型：输入输出均为序列数据的模型。序列模型将输入序列转换为目标序列数据。

RNN:

  • 按序列计算，不能并行化
  • 对长短期依赖关系没有明显的建模
  • 通过一个隐藏层状态不能完全表征局部和全局的信息

CNN

  • 很容易捕捉局部依赖
  • 可以并行化
  • 远程依赖需要多个layers

RNN with Attention

  • 解决了解码器-编码器的瓶颈

注意力机制

  1. Encode 所有输入序列，得到对应的representation $h_1 h_2$ $\mathrm{h}3 \ldots \ldots \mathrm{h}{\mathrm{T}}$ ( $\mathrm{T}$ 为输入序列的长度 )
  2. Decode输出目标 $y_t$ 之前，会将上一步输出的隐藏状态 $S_{t-1}$ 与之 前encode好的representation进行对比，计算相似度 $\left(e_{t, j}=\right.$ $a\left(s_{t-1}, h_j\right) ， h_j$ 为之前第 个输入字符encode得到的隐臧向量， $a$ 为任意一种计算相似度的方式 )
  3. 然后再通过softmax， $a_{t, j}=\frac{\exp \left(e_{t, j}\right)}{\sum_{k=1}^{T_x} \exp \left(e_{t, k}\right)}$ 将之前得到的各个部 分的相关系数进行归一化，得到 $a_{t, 1} a_{t, 2} a_{t, 3} \ldots \ldots a_{t, T}$
  4. 再对输入序列的隐藏层进行相关性加权求和得到此时 decode需 要的context vector $c_j=\sum_{j=1}^{T_x} a_{i, j} h_j$

注意力机制和自注意力机制区别

attention

\[\begin{aligned} \mathbf{h}_i &=\operatorname{attenion}\left((K, V), q_i\right) \\ &=\sum_{j=1}^N \alpha_{i j} v_j \\ &=\sum_{j=1}^N \operatorname{softmax}\left(s\left(k_j, q_i\right)\right) v_j \end{aligned}\]

self-attention \(\mathrm{H}=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V\)

总结： Attention的query来自外部序列，Self-Attention的query来自于原本的序列

自注意力机制和卷积网络区别

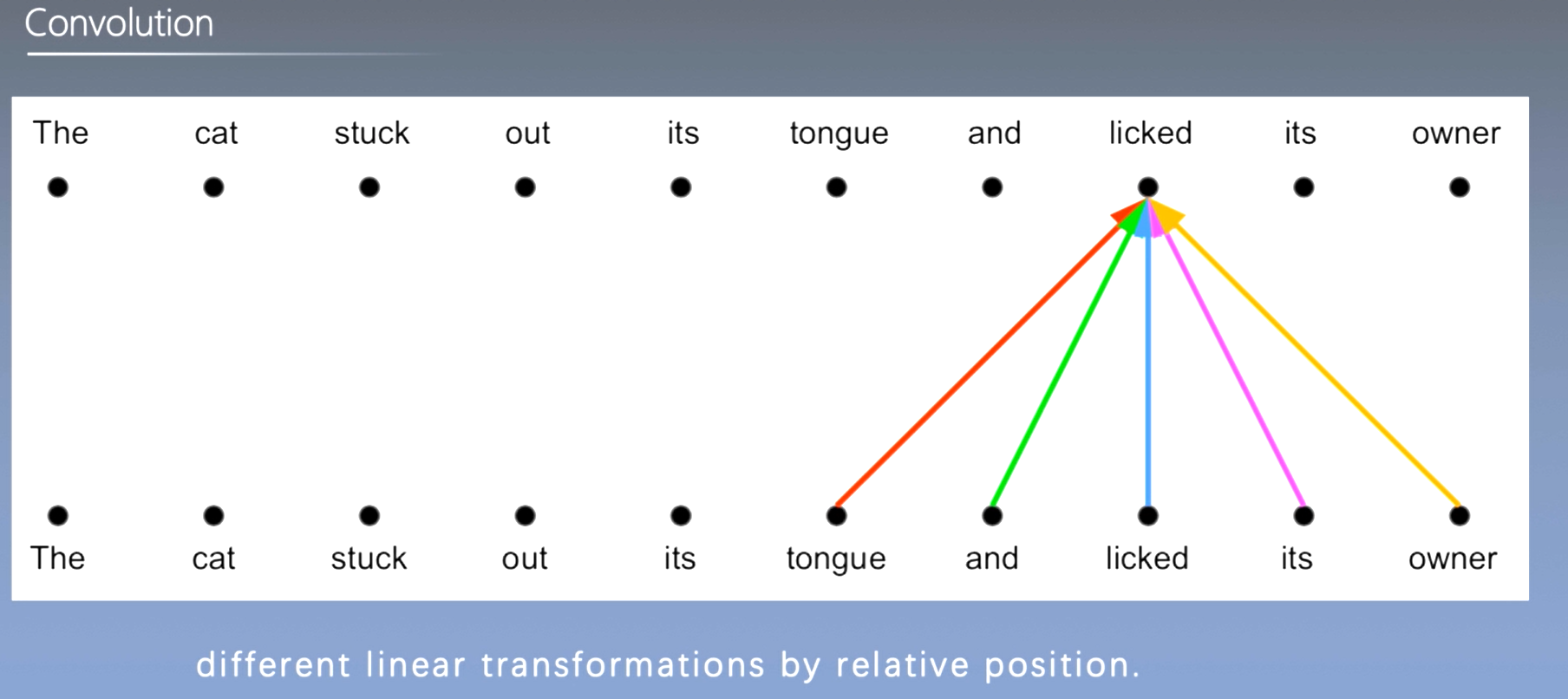
20220920153448-2022-09-20-15-34-48

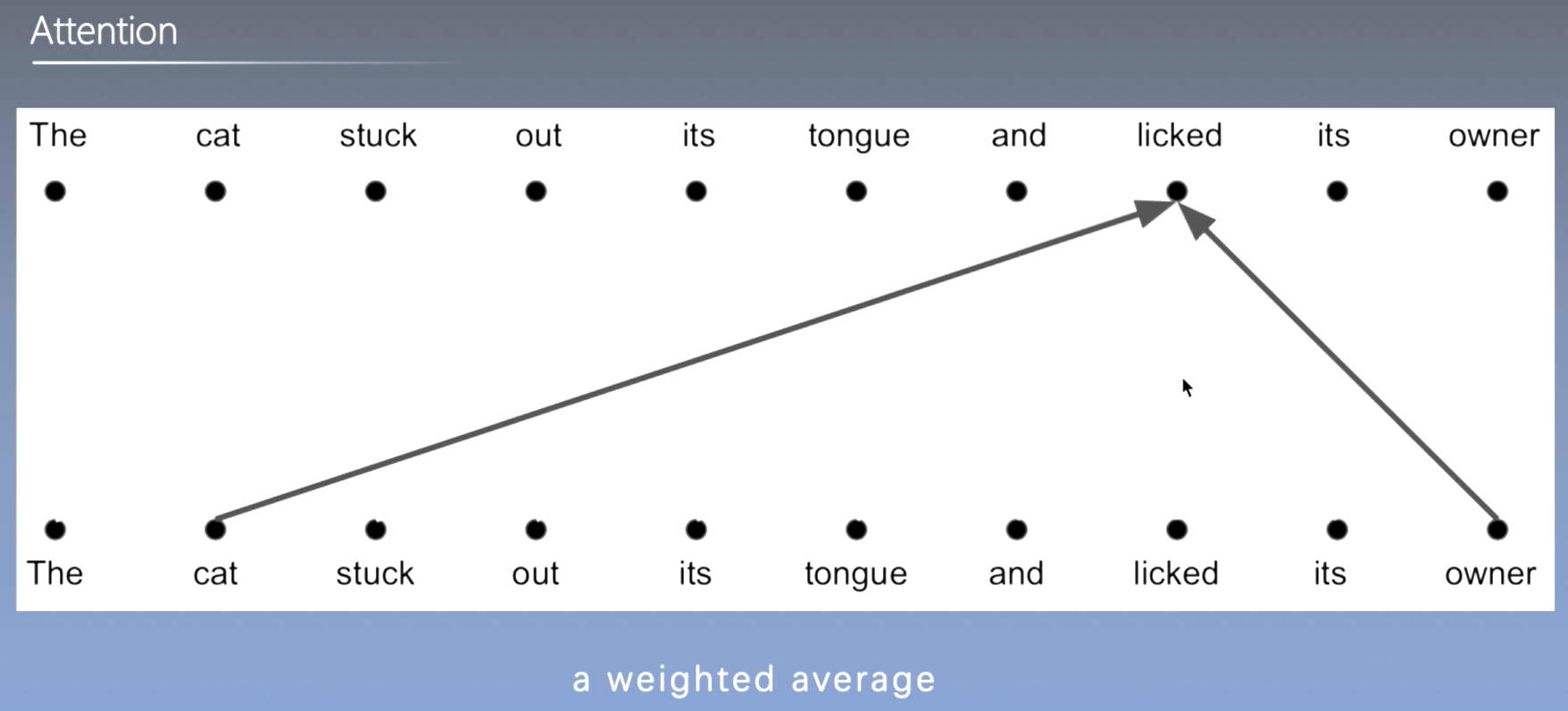
20220920153521-2022-09-20-15-35-22

20220920153540-2022-09-20-15-35-41

  • 自注意力机制视野区域可变，可通过多头注意力学习到多通道信息
  • CNN通过多个卷积核可以学到多通道的信息

MultiHead $(Q, K, V)=$ Concat $\left(\right.$ head $_1, \ldots$, head $\left._h\right) W^o$ where head $_i=$ Attention $\left(Q W_i^Q, K W_i^K, V W_i^V\right)$

\[\begin{gathered} w_i^Q \in \mathbb{R}^{d_{\text {model }} \times d_k} \\ w_i{ }^K \in \mathbb{R}^{d_{\text {model }} \times d_k} \\ w_i^V \in \mathbb{R}^{d_{\text {model }} \times d_v} \\ w^0 \in \mathbb{R}^{h d_v \times d_{\text {model }}} \\ d_k=d_v=\frac{d_{\text {model }}}{h}=64 \end{gathered}\]

摘要

  • 问题（现状）是什么？
    • 占主导地位的序列转换模型是基于复杂的递归或卷积神经网络，包括一个编码器和一个解码器。性能最好的模型还通过注意机制将编码器和解码器连接起来。
  • 我们要做什么？
    • 我们提出了一个新的简单的网络结构–Transformer，它完全基于注意力机制，完全不需要递归和卷积
  • 大概怎么做的
  • 实验效果
    • 在两个机器翻译任务上的实验表明，这些模型在质量上更胜一筹，同时更容易并行化，所需的训练时间也大大减少。我们的模型在WMT 2014英德翻译任务中达到了28.4 BLEU，比现有的最佳结果（包括合集）提高了2 BLEU以上。在WMT 2014英法翻译任务中，我们的模型在8个GPU上训练了3.5天后，建立了新的单模型最先进的BLEU得分，即41.8分，只是文献中最佳模型的训练成本的一小部分。我们通过将其成功地应用于有大量和有限训练数据的英语选区解析，表明Transformer可以很好地推广到其他任务。

介绍

按照起承转合的思想阅读。

  • 起。做的哪方面工作？
    • 递归神经网络，特别是长短时记忆和门控递归神经网络，已经被牢固地确立为序列建模和序列转换的最先进方法。
  • 承。相关工作
    • 递归模型通常沿着输入和输出序列的符号位置进行计算。将这些位置与计算时间的步骤对齐，它们产生一个隐藏状态的序列$h_t$，作为前一个隐藏状态$h_{t-1}$和位置t的输入的函数。这种固有的顺序性排除了训练实例内的并行化，这在较长的序列长度上变得至关重要，因为内存限制了跨实例的批处理。
  • 转。相关工作的不足和转机
    • 最近的工作通过因式分解技巧和条件计算在计算效率方面取得了重大改进，同时在后者的情况下也提高了模型性能。然而，顺序计算的基本约束仍然存在。
    • 注意机制已经成为各种任务中引人注目的序列建模和转换模型的一个组成部分，允许对依赖关系进行建模，而不考虑它们在输入或输出序列中的距离。然而，除了少数情况外，这种注意机制是与递归网络结合使用的。
  • 合。本文工作
    • 在这项工作中，我们提出了Transformer，这是一个摒弃递归的模型架构，而完全依靠注意力机制来得出输入和输出之间的全局依赖关系。
    • Transformer允许显著提高并行化程度，并且在8个P100 GPU上经过短短12个小时的训练，就可以达到翻译质量的新水平。

相关工作

主要介绍背景知识。

减少顺序计算的目标也构成了扩展神经GPU、ByteNet和ConvS2S的基础，它们都使用卷积神经网络作为基本构件，对所有输入和输出位置并行计算隐藏表征。在这些模型中，将来自两个任意输入或输出位置的信号联系起来所需的操作数量随着位置之间的距离增长，对于ConvS2S是线性增长，对于ByteNet是对数增长。这使得学习遥远位置之间的依赖关系更加困难。在Transformer中，这被减少到一个恒定的操作数，尽管代价是由于注意力加权位置的平均化而降低了有效的分辨率，我们用多头注意力抵消了这一影响。

自注意力机制，有时也被称为内部注意，是一种与单个序列的不同位置相关的注意机制，以计算该序列的表示。自注意力已被成功地用于各种任务，包括阅读理解、抽象概括、文本连带和学习与任务无关的句子表示。

端到端记忆网络是基于递归注意机制，而不是序列排列的递归，并已被证明在简单语言问题回答和语言建模任务中表现良好。

然而，据我们所知，Transformer是第一个完全依靠自我注意来计算其输入和输出的表征，而不使用序列对齐的RNN或卷积的转换模型。

方法

  • 简要地重复问题
  • 解决思路
  • 必要的形式化定义
  • 具体模型

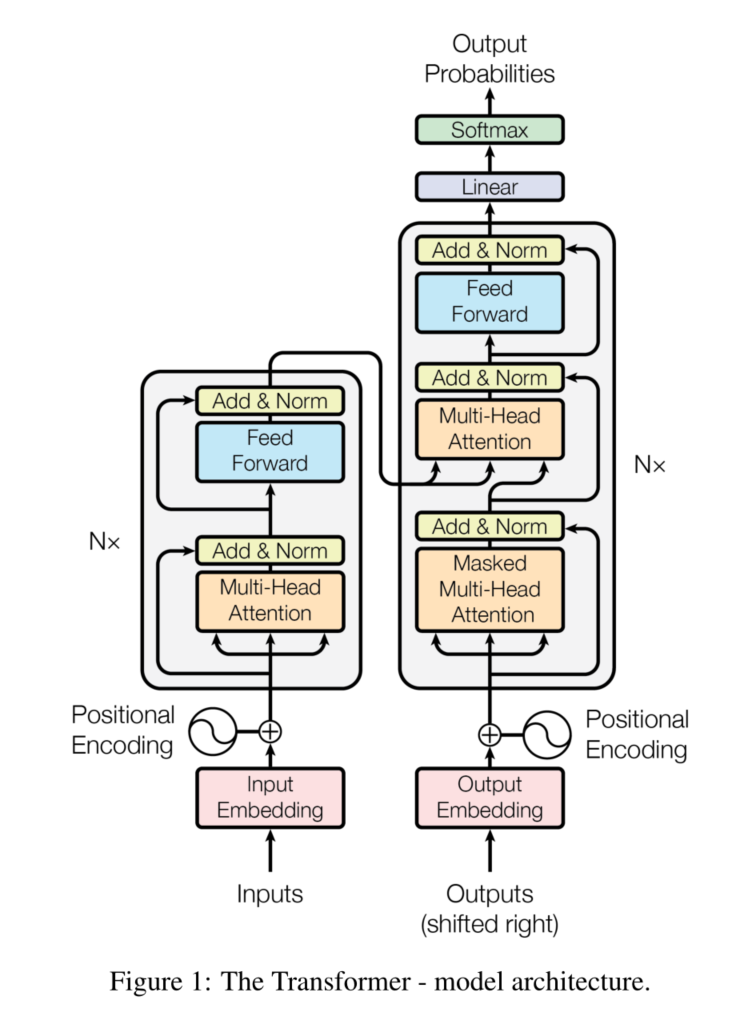
20220919223428-2022-09-19-22-34-30

编码器与解码器区别

MASK

  • 编码器编码整个序列
  • 解码只能一个个字符来解码

实验

  • 数据集和实验设置

  • 主实验，提供详尽的实验分析

    • Machine Translation
      • 在数据集WMT 2014上表现SOTA
    • English Constituency Parsing
      • 在数据集WSJ 23上表现SOTA

讨论与总结

  1. 如何实现并行计算同时缩短依赖距离？ 答：采用注意力机制。
  2. 如何像CNN一样考虑到多通道信息？ 答：采用多头注意力机制。
  3. 自注意力机制损失了位置信息，如何补偿？ 答：位置嵌入。
  4. 后面的层中位置信息消散 答：残差连接。
  5. 为什么要残差连接？ 答：残差可以将位置信息映射到高层。位置信息最初添加在了模型的输入处，通过残差连接将位置信息传递到每一层，可以不需要再每一层都添加位置信息。

20220920214928-2022-09-20-21-49-29