协方差
什么是协方差
协方差是用于衡量两个变量的总体误差。假设两个变量分别是x和y,而它们的采样数量都是m,那么协方差的计 算公式就是如下这种形式
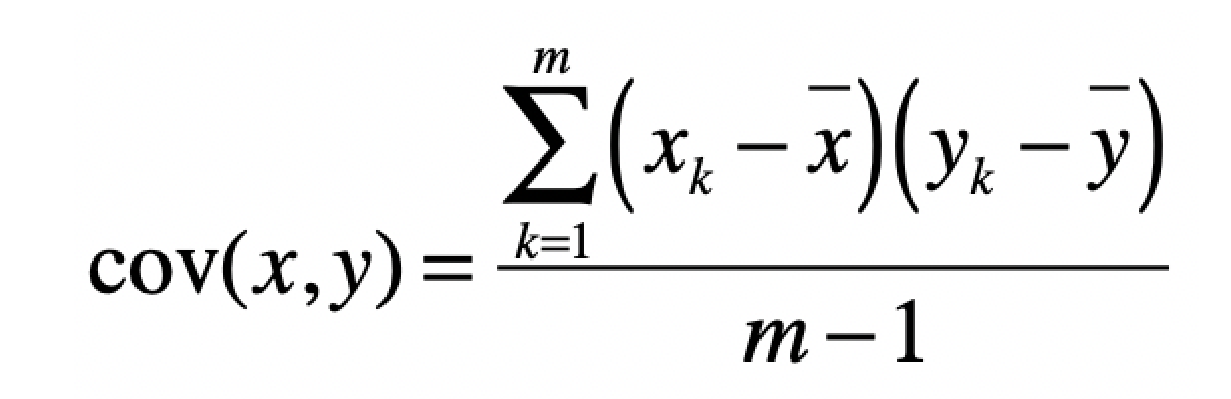
其中\(x_k\)示变量\(x\)的第\(k\)个采样数据, \(\bar{x}\)表示这\(k\)个采样的平均值。而当两个变量是相同 时,协方差就变成了方差。
假设\(X_{,1}\)表示样本矩阵\(X\)的第1列,\(X_{,2}\)表示样本矩阵\(X\)的第2列,依次类推。而\(cover(X_{,1},X_{,1})\)表示第 1 列向量和自己的协方差,而\(cover(X_{,1},X_{,2})\)表示第 1 列向量和第 2 列向量之间的协方差。结合之前 协方差的定义,我们可以得知:
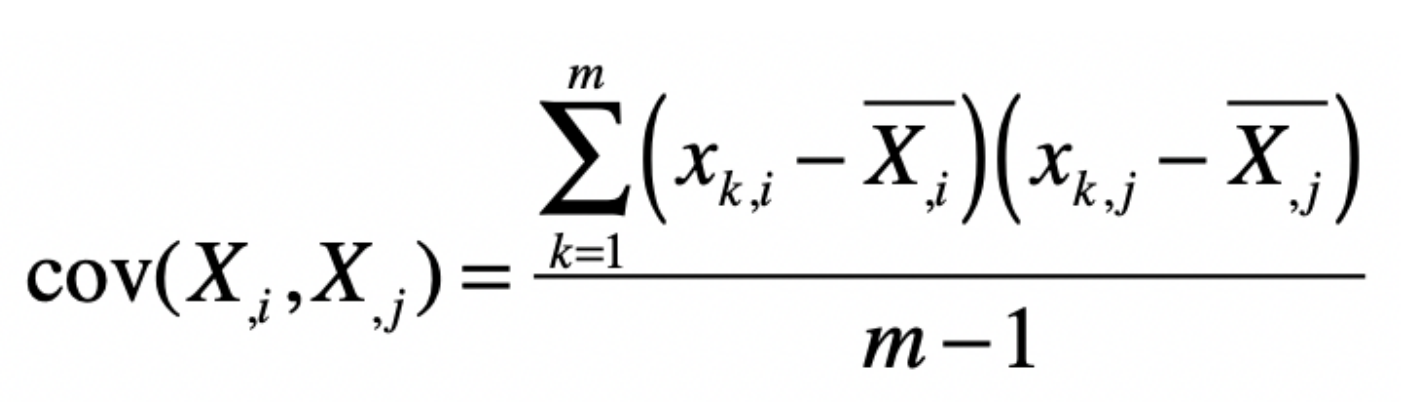
其中, \(X_{k,i}\)表示矩阵中第k行,第i列的元素。 \(\bar{X_{,i}}\)表示第\(i\)列的平均值。
有了这些符号表示,我们就可以生成下面这种协方差矩阵。
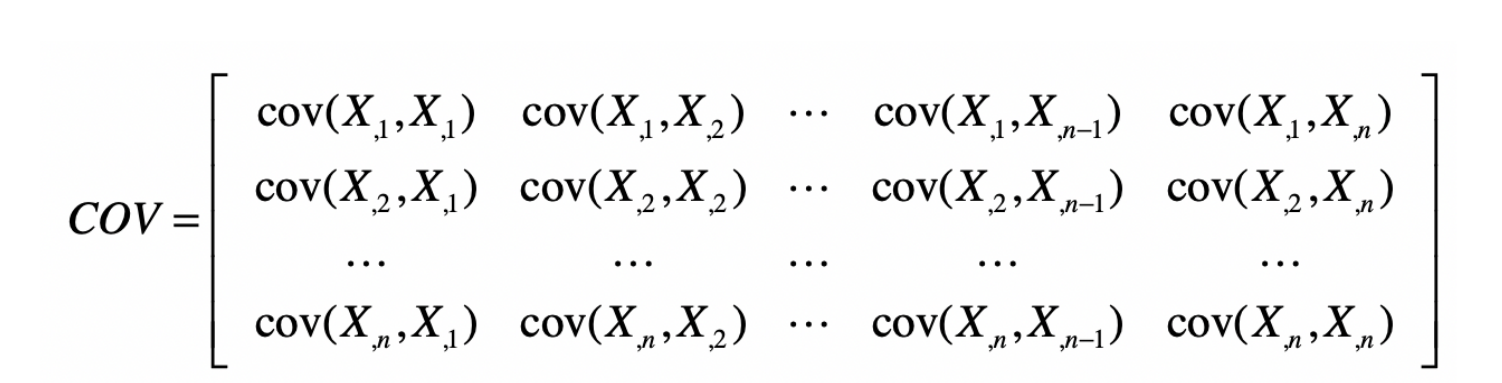
从协方差的定义可以看出,\(cover(X_{,i},X_{,j})=cover(X_{,j},X_{,i})\) ,所以COV是个对称矩阵。 另外,我们刚刚提到,对于\(cover(X_{,i},X_{,j})\),如果\(i=j\),那么\(cover(X_{,i},X_{,j})\)也就是\(X_{,j}\)这组数的方差。所以这个对称矩阵的主对角线上的值就是各维特征的方差。