087

英文名称： Prompt Consistency for Zero-Shot Task Generalization

中文名称： 零样本任务泛化的提示一致性

论文地址： https://arxiv.org/abs/2205.00049

期刊/时间： 2022

论文地址： https://github.com/violet-zct/swarm-distillation-zero-shot

代码地址： https://github.com/violet-zct/swarm-distillation-zero-shot?utm_source=catalyzex.com

前置知识

摘要

• 问题是什么？
  • 最近NLP历史上最令人印象深刻的结果之一是，预先训练好的语言模型有能力在零样本的环境中解决新的任务。为了实现这一点，NLP任务被框定为自然语言提示，产生一个表明预测输出的响应。尽管如此，在这样的环境下，其性能往往远远落后于其监督数据集，这表明有很大的潜在改进空间。
• 我们要做什么？
  • 在本文中，我们探索了利用无标签数据来提高零样本的性能的方法。
• 大概怎么做的
  • 具体来说，我们利用了多个提示可以用来指定一个任务的事实，并建议对提示的一致性进行规范化处理，鼓励对这个不同的提示集进行一致的预测。我们的方法可以通过额外的无标记训练数据对模型进行微调，或者在推理时以无监督的方式直接对测试输入进行微调。
• 实验效果
  • 在实验中，我们的方法在4个NLP任务的11个数据集中的9个上超过了最先进的零样本学习器T0（Sanh等人，2022），准确率高达10.6个绝对点。这些收益通常是在少量未标记的例子中获得的。

介绍

按照起承转合的思想阅读。

• 起。做的哪方面工作？
  • 过去十年已经证明，预训练语言模型（PLM）是改善从训练数据集到测试数据集的泛化的有力工具（Devlin等人，2019；Liu等人，2019；Raffel等人，2020）
• 承。相关工作
  • 而最近的工作表明，它们甚至可以在没有任何注释实例的情况下对新任务进行零样本泛化（Brown等人，2020；Wei等人，2022；Sanh等人，2022）。这些系统利用自然语言提示，为模型指定任务，并以统一的格式表示不同的任务。零样本任务泛化提出了一条通往通用系统的道路，该系统可以在没有注释的情况下执行各种NLP任务。
• 转。相关工作的不足和转机
  • 虽然在概念上很诱人，但与使用少量特定任务标签数据训练的系统相比，零样本的性能往往仍然比较低。
• 合。本文工作
  • 在本文中，我们研究了使用无标签文本使PLM更好地进行零样本学习的方法。我们的工作受到一致性训练方法的激励，该方法将模型预测正则化，使之不受扰动影响。一致性训练作为利用未注释实例的有效技术，在半监督学习文献中被广泛使用（Bachman等人，2014；Sajjadi等人，2016；Beyer等人，2019；Xie等人，2020a）。它通常被理解为一种平滑度正则化或数据增强（Xie等人，2020a），并在半监督学习中获得了强大的性能。
  • 我们建议对提示一致性进行正则化，即模型被正则化，以便在一组不同的同义任务提示中做出相同的预测，而不是例子层面的一致性。提示性一致性正则化在直觉上是有意义的，因为PLM在同义提示中应该是鲁棒的，而根据经验，模型的预测对任务提示的wording非常敏感（Jiang等人，2020）。
  • 具体来说，我们设计了一个成对的蒸馏损失，鼓励每一对提示之间的一致性（图1）。我们把我们的方法称为swarm distillation，它的优点是完全无监督，只需要未注释的输入。值得注意的是，未加注释的例子通常比较容易收集。为一个任务起草几个提示语也比为每个例子注释标签要便宜得多，事实上，已经有精心设计的提示语可用于广泛的NLP任务（Bach等人，2022）。
  • 以前关于实例级一致性正则化的工作通常通过最小化在半监督环境下的一致性损失与监督损失（Miyato等人，2018；Xie等人，2020a）。最近，Elazar等人（2021年）在关系预测任务的背景下进行了优化提示一致性损失的实验，同时还结合了监督版的掩蔽语言模型预训练目标。相比之下，我们（1）单独优化了一个新的提示性一致性损失，使我们的方法完全无监督，并且与模型的预训练目标无关，以及（2）在广泛的NLP任务中实验并证明了这种方法的实用性。值得注意的是，这种无监督的设置带来了额外的学习挑战：如果没有明确的监督，模型可能会遭受灾难性的遗忘，甚至表现出一种崩溃的形式，即模型对任何输入都会做出相同的预测。
  • 为了解决这个问题，我们采取了两个简单的策略：（1）我们利用参数高效的tuning技术（Houlsby等人，2019年；He等人，2022年），只更新少量的额外参数，通过固定原始PLM参数自然地缓解灾难性遗忘；（2）我们提出一个无监督的标准，用于在模型落入崩溃的局部最优之前选择检查点
  • 在实验中，我们将我们的方法建立在最先进的零样本任务学习者T0（Sanh等人，2022）之上，并在来自4个NLP任务的11个数据集上验证其性能：自然语言推理、核心推理解析、词义歧义和句子完成。我们在两种情况下进行了实验。(1) 用未标记的训练数据训练模型；或直接在未标记的测试输入上调整模型。
  • 在这两种情况下，我们表明我们的swarm distillation方法在11个数据集中的9个上提高了3B参数T0模型的精度，绝对值高达10.6分。我们进一步将模型规模扩大到11B参数，并证明我们的方法在4个数据集中的4个上优于11B参数的T0模型。值得注意的是，分析表明，这些收益往往只需要几十个例子就能实现，这表明计算开销很小。

相关工作

主要介绍背景知识。

方法

• 简要地重复问题
• 解决思路
• 必要的形式化定义
• 具体模型

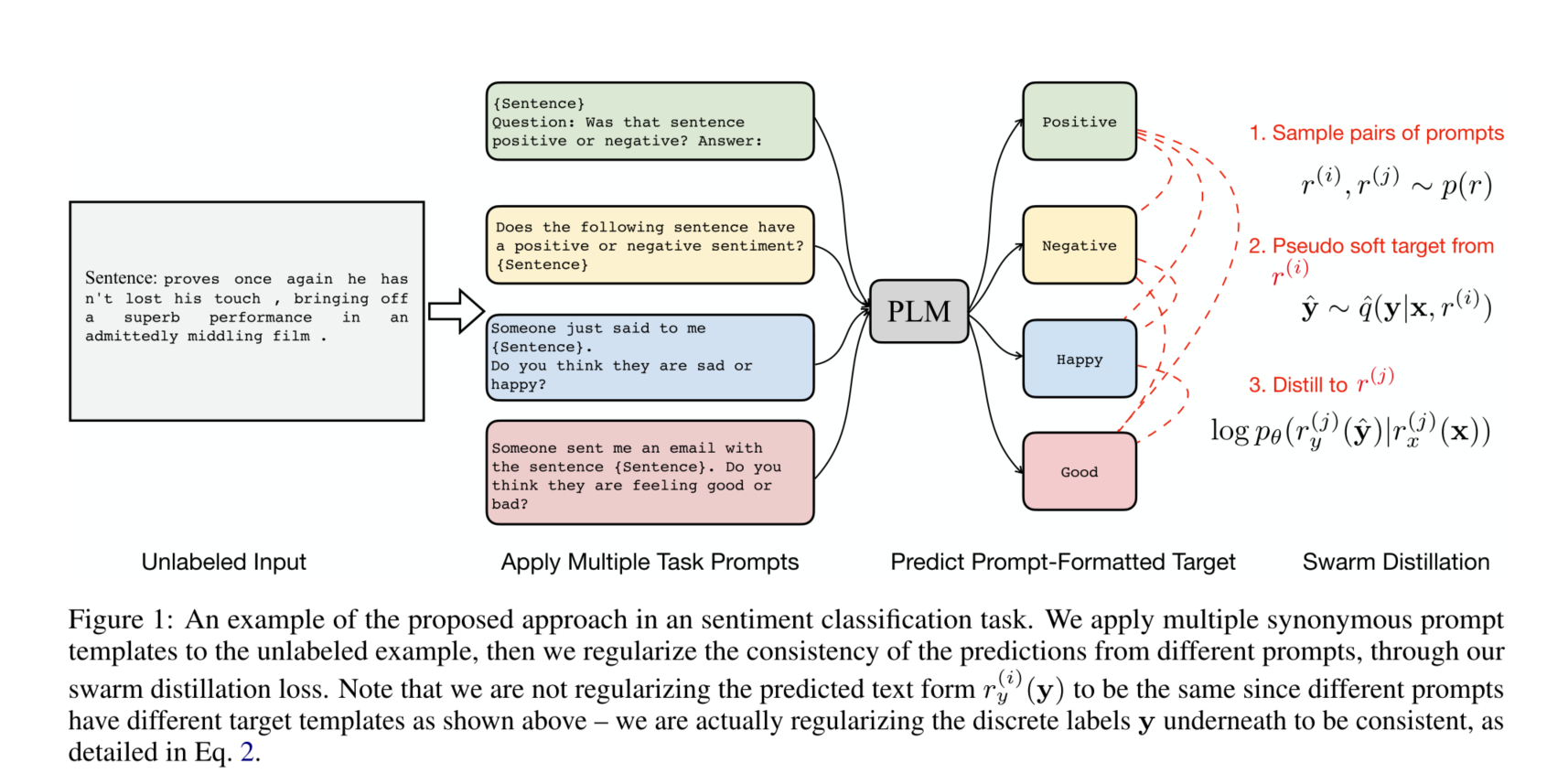
对于一个新任务任务，有输入集合 $\left{\mathrm{x}_1, \mathrm{x}_2, \ldots, \mathrm{x}_N\right}$ ，和K个不同的prompt $\left{\left(r_x^{(1)}, r_y^{(1)}\right), \ldots,\left(r_x^{(K)}, r_y^{(K)}\right)\right}$ 。本文的目的是无监督学习函数 $f: \mathcal{X} \rightarrow \mathcal{Y}$ 。

无标签的输入在实践中经常出现，我们在文中考虑了两种这样的情况。

• 第一种情况：非测试集的未注释的例子可用
• 第二种情况：当未注释的测试输入可用

以前的方法使用一个额外的模块来扰乱每个例子，然后优化例子级的一致性，而我们建议优化提示级的一致性，这（1）在概念上是简单的，（2）可以缓解PLM的预测通常与同一任务的不同提示不一致的事实。我们建议将不同的提示对给定输入的预测正则化，使其相互接近，使用成对的蒸馏损失来使一个提示的预测更接近另一个提示的预测。

作者希望同一个数据的不同prompt，在infer的时候，能得到相同的结果。将这个想法作为约束， 就能在无监督数据上训练模型。损失函数为:损失函数定义为：

\[\begin{aligned} \mathcal{L}=-& \mathbb{E}_{\mathbf{x} \sim p_d(\mathbf{x})} \mathbb{E}_{r^{(i)}, r}(j) \sim p(r) \\ & \mathbb{E}_{\hat{\mathbf{y}} \sim \hat{q}\left(\mathbf{y} \mid \mathbf{x}, r^{(i)}\right)} \log p_\theta\left(r_y^{(j)}(\hat{\mathbf{y}}) \mid r_x^{(j)}(\mathbf{x})\right) \end{aligned}\]

$p_d(\mathrm{x})$ 是输入数据的分布， $p(r)$ 是prompt的分布。

对于这个损失函数的理解：对于同一个数据，不同prompt都有一个对于标签对预测分布，该损失约束要求不同标签间的这个分布差异要尽量小。

在成对一致性损失中停止一方的梯度，也被证明有助于缓解所有输入导致相同预测的崩溃问题。

与传统的从教师模型提炼到学生模型的提炼（Hinton等人，2015），或以前的一致性训练，即一个教师提炼到几个学生（Clark等人，2018；Xie等人，2020a）不同，我们在一群提示中两两比较进行提炼，每个提示同时是教师和学生，因此我们把我们的方法称为swarm distillation。在我们的实施中，我们用k个随机抽样的提示对来近似期望值（r(i), r(j)），而不是列举所有的提示对来提高训练效率。

直接这样训练整个网络可能佘使得模型坍塌（collapse)，即模型会进入对所有输入，所有 prompt都预测同一个标签的局部最优，来获得一个较高的一致性。

为了避免这个情况，作者采用LoRA模块，新增了一部分可训练参数，保持原网络fix。

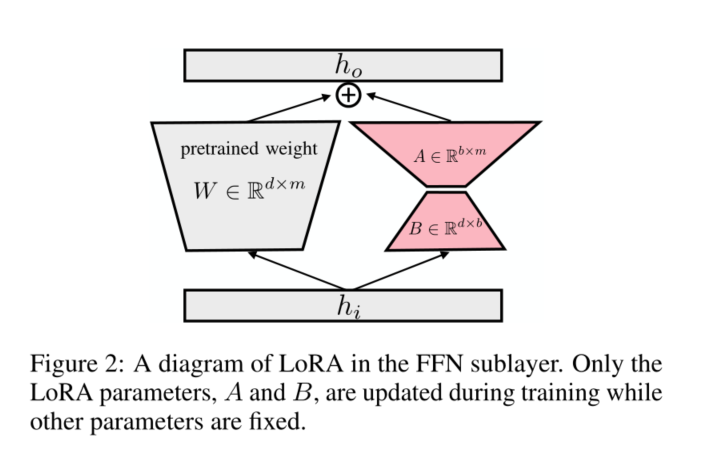
具体来说，即在预训练好的transformer的每一层的FNN的weight $W$ 中，加入新的参数，将其变 为 $W+\alpha B A ， W$ 不更新，只更新 $B$ 和 $A$ 。

停止策略

由于没有valid集，作者设计了一个训练停止条件，利用Fleiss Kappa指标来衡量预测的一致性。Fleiss'kappa表示，如果所有的提示都按照标签的边缘化分布进行预测，那么提示之间的一致程度就会超过预期的程度。 \(p_i=\frac{1}{K(K-1)} \sum_j n_{i j}\left(n_{i j}-1\right),\) $n_{i j}$ 是模型对第 $i$ 个数据的第 $j$ 标签的预测的prompt个数， $K$ 是prompt的个数。则 $p_i$ 反映了 对第 $i$ 个数据的预测的一致性， $p_i$ 越高，一致性越强。

\(\bar{P}_e=\sum_j q_j^2, \quad q_j=\frac{1}{N K} \sum_{i=1}^N n_{i j},\) $\bar{P}_e$ 反映了模型对所有数据中，标签分布的极性。若模型只预测一个标签， $\bar{P}_e$ 最大，此时即上述所说的坍塌。 Fleiss Kappa指标计算为: $\kappa=\frac{\bar{P}-\bar{P}_e}{1-\bar{P}_e}$ 作者在 $\kappa$ 开始单调递减是停止训练。

实验

• 数据集和实验设置
• 主实验，提供详尽的实验分析

在数据集上表现SOTA

讨论与总结

在本文中，我们探索了提示一致性正则化，使PLM成为更好的零样本学习者。我们的方法利用未标记的例子来达到零样本的收益。虽然我们以后适应的方式使用它来适应PLM与所提出的swarm distillation，但我们的正则化损失有可能与预训练阶段的预训练目标相结合，与多提示训练损失（Sanh等人，2022；Wei等人，2022）相结合，甚至与少样本学习设置的注释数据相结合。将swarm distillation与这些其他损失结合起来，可以很容易地绕过模型崩溃的问题，因为其他损失通常不鼓励崩溃的局部最优。 无监督swarm distillation法在序列生成任务上的潜在应用也值得在未来进行研究