2.词向量进阶

20221001202122-2022-10-01-20-21-23

1.word2vec主要思想

  • 模型会遍历整个语料库中的每个单词
  • 使用中心单词向量预测周围的单词（Skip-Gram）
\[P(o \mid c)=\frac{\exp \left(u_o^T v_c\right)}{\sum_{w \in V} \exp \left(u_w^T v_c\right)}\]

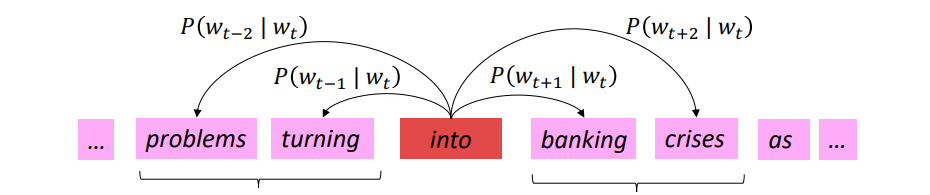
20221001203205-2022-10-01-20-32-06

仅该算法学习的单词向量能很好地捕捉单词的相似性和单词空间中的有意义的方向

  • $U 、 V$ 矩阵，每行代表一个单词的词向量，点乘后得到的分数通过softmax映射为概率分布。得到的概率分布是对于该中心词而言的上下文中单词的概率分布，该分布与上下文所在的具体位置无关，所以在每个位置的预测都是一样的。

1.1 优化算法：梯度下降

  • 我们有需要最小化的代价函数 $J(\theta)$
  • 我们使用梯度下降算法最小化 $J(\theta)$
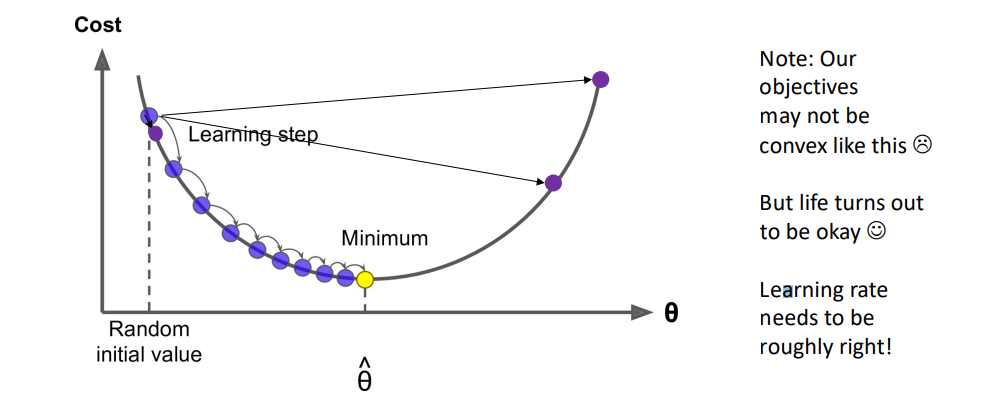
  • 遵循梯度下降的一般思路，我们计算 $\theta$对于参数 $J(\theta)$ 的梯度，然后朝着负梯度的方向迈进一小步，并不断重复这个过程，如图所示。

20221001204006-2022-10-01-20-40-06

1.2 更多细节

  • 为什么是两个向量
    • 更容易优化，在最后进行平均。
  • 两个模型变种
    • Skip-grams (SG)：通过给定中心词预测上下文的内容
    • Continuous Bag of Words (CBOW)：从上下文单词预测中心词
  • 在训练中添加效率
    • 负采样（Negative sampling）

负采样算法

2.1 负例采样的skip-gram模型

softmax中用于归一化的分母的计算代价太高 \(P(o \mid c)=\frac{\exp \left(u_o^T v_c\right)}{\sum_{w \in V} \exp \left(u_w^T v_c\right)}\)

  • 我们将实现使用 negative sampling/负例采样方法的 skip-gram 模型。

  • 主要思想：使用一个 true pair (中心词及其上下文窗口中的词)与几个 noise pair (中心词与随机词搭配) 形成的样本， 训练二元逻辑回归。

  • 原文中的(最大化)目标函数是 $J(\theta)=\frac{1}{T} \sum_{t=1}^T J_t(\theta) J_t(\theta)=\log \sigma\left(u_o^T v_c\right)+\sum_{i=1}^k \mathbb{E}_{j \sim P(w)}\left[\log \sigma\left(-u_j^T v_c\right)\right]$

  • 我们要最大化2个词共现的概率

目标函数是 \(J_{\text {neg-sample }}\left(\boldsymbol{o}, \boldsymbol{v}_c, \boldsymbol{U}\right)=-\log \left(\sigma\left(\boldsymbol{u}_o^{\top} \boldsymbol{v}_c\right)\right)-\sum_{k=1}^K \log \left(\sigma\left(-\boldsymbol{u}_k^{\top} \boldsymbol{v}_c\right)\right)\)

  • 我们取 $k$ 个负例采样
  • 最大化窗口中包围「中心词」的这些词语出现的概率，而最小化其他没有出现的随机词的概率 $P(w)=U(w)^{3 / 4} / Z$
  • 我们用上述公式进行抽样，其中 $U(w)$ 是 unigram 分布
  • 通过 3/4 次方，相对减少常见单词的频率，增大稀有词的概率
  • $Z$ 用于生成概率分布

3.共现矩阵

3.1 共现矩阵与词向量构建

迭代整个语料库（也许是很多次）有一些奇怪的地方；为什么我们不直接积累所有的统计数字，即哪些词出现在彼此附近呢！？

构建共现矩阵$X$

  • 2个选项：窗口与完整文档
  • Windows。类似于word2vec，在每个词周围使用Windows,捕获一些句法和语义信息（"词空间"）
  • Word-document 共现矩阵将给出一般的主题（所有体育术语都有类似的条目），这一构建单词文章co-occurrence matrix的方法也是经典的Latent Semantic Analysis所采用的【语义分析】。

3.2 基于窗口的共现矩阵示例

  • 窗口长度为1（更常见的是：5-10）
  • 对称性（与左或右的内容无关）

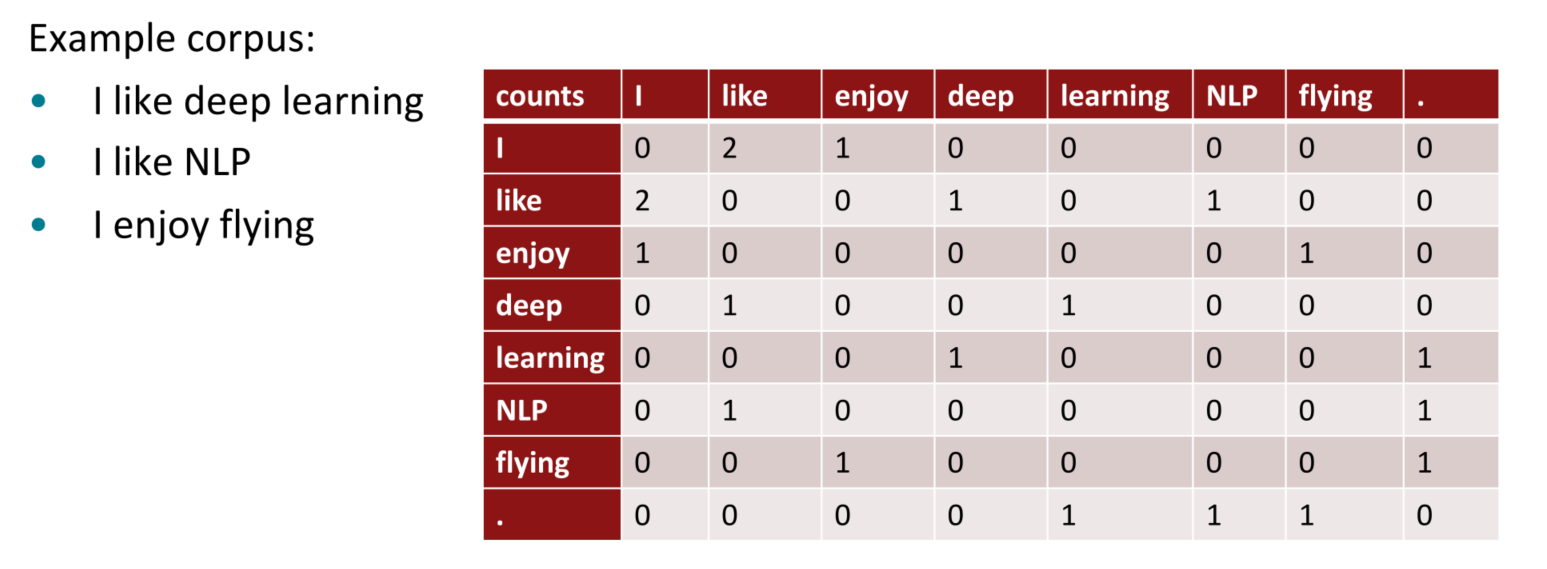
20221001205550-2022-10-01-20-55-51

3.3 基于直接的共现矩阵构建词向量

基于直接的共现矩阵构建词向量

  • 向量的大小随着词汇量的增加而增加
  • 维度非常高：需要大量的存储（尽管是稀疏的）
  • 后续的分类模型也会由于矩阵的稀疏性而存在稀疏性问题，使得效果不佳。->模型不具备鲁棒性

3.4 解决方案：低维向量

低维向量

  • 思路：将 "大部分 "重要信息存储在一个固定的、少量的维度中：密集向量
  • 通常是25-1000维，类似于word2vec
  • 如何降低维度？

3.5 方法1：对X进行降维

可以使用SVD方法将共现矩阵 $X$ 分解为 $U \Sigma V^T$ ，其中:

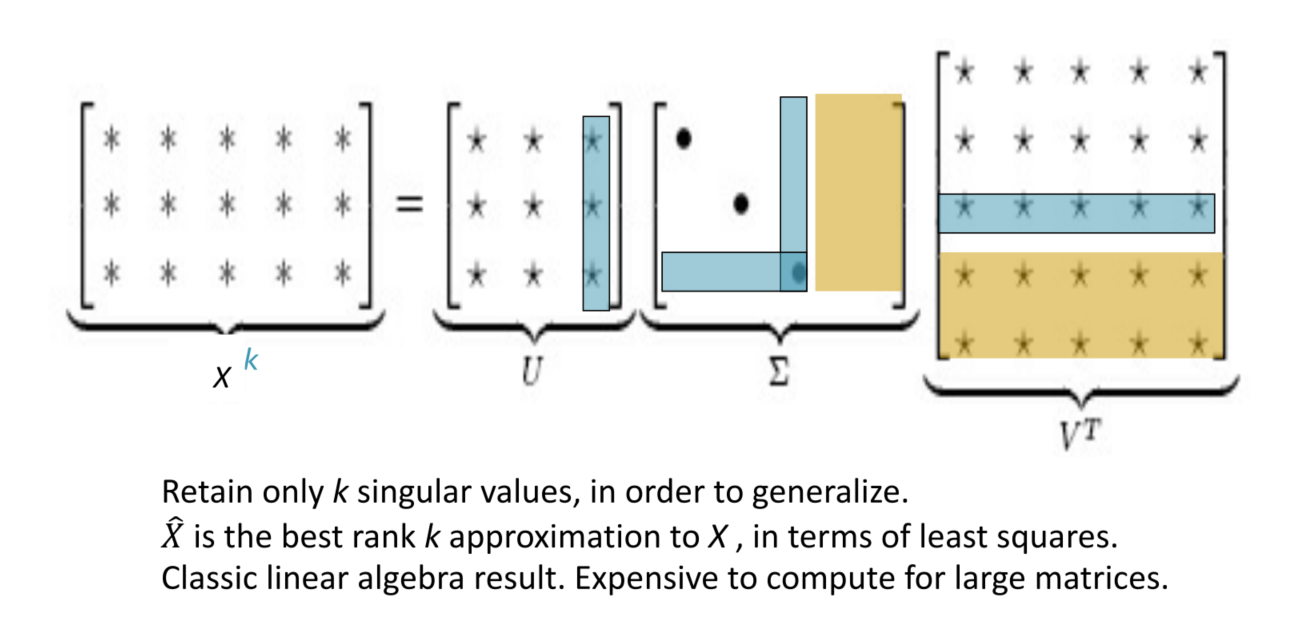
20221001214008-2022-10-01-21-40-09

  • $\Sigma$ 是对角线矩阵，对角线上的值是矩阵的奇异值
  • $U, V$ 是对应于行和列的正交基 为了减少尺度同时尽量保存有效信息，可保留对角矩阵的最大的 $k$ 个值，并将矩阵 $U, V$ 的相应的行列保留。
  • 这是经典的线性代数算法，对于大型矩阵而言，计算代价昂贵。

3.6 基于计数 VS. 基于预估

基于计数：使用整个矩阵的全局统计数据来直接估计

  • 优点：训练快速；统计数据高效利用
  • 缺点：主要用于捕捉单词相似性；对大量数据给予比例失调的重视

基于预估模型：定义概率分布并试图预测单词

  • 优点：提高其他任务的性能；能捕获除了单词相似性以外的复杂的模式
  • 缺点：随语料库增大会增大规模；统计数据的低效使用（采样是对统计数据的低效使用）

4.GloVe模型

GloVe模型关键思想：共现概率的比值可以对meaning component进行编码。将两个流派的想法结合起来，在神经网络中使用计数矩阵。

  • 优点
    • 训练快速
    • 可以扩展到大型语料库
    • 即使是小语料库和小向量，性能也很好

5.词向量评估

如何评估词向量？

我们如何评估词向量呢，有内在和外在两种方式：

  • 内在评估方式
    • 对特定/中间子任务进行评估
    • 计算速度快
    • 有助于理解这个系统
    • 不清楚是否真的有用，除非与实际任务建立了相关性
  • 外部任务方式
    • 对真实任务（如下游NLP任务）的评估
    • 计算精确度可能需要很长时间
    • 不清楚子系统问题所在，是交互还是其他子系统问题
    • 如果用另一个子系统替换一个子系统可以提高精确度

5.2 内在词向量评估

一种内在词向量评估方式是「词向量类比」：对于具备某种关系的词对a,b，在给定词c的情况下，找到具备类似关系的词d \(a: b:: c: ? \rightarrow d=\arg \max _i \frac{\left(x_b-x_a+x_c\right)^T x_i}{\left\|x_b-x_a+x_c\right\|}\)

  • 通过加法后的余弦距离是否能很好地捕捉到直观的语义和句法类比问题来评估单词向量
  • 从搜索中丟弃输入的单词
  • 问题:如果有信息但不是线性的怎么办?

5.3 另一个内在词向量评估

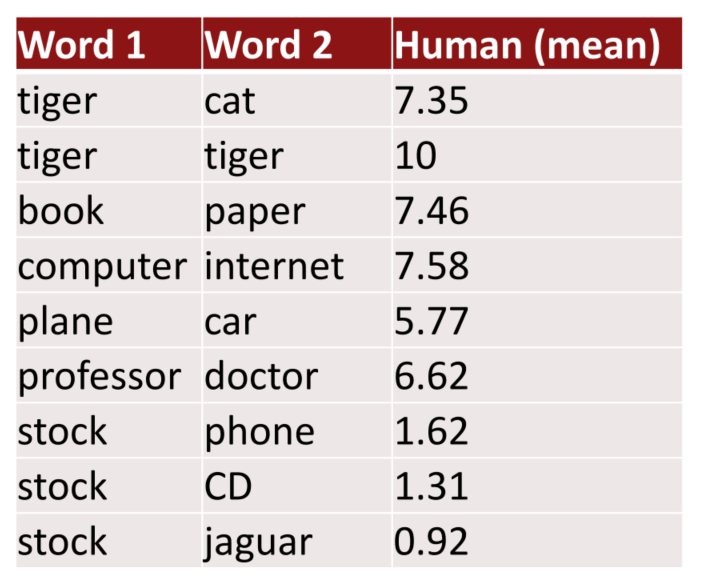
20221001215253-2022-10-01-21-52-54

  • 使用 cosine similarity 衡量词向量之间的相似程度
  • 并与人类评估比照

5.3 外向词向量评估

单词向量的外部评估：词向量可以应用于NLP的很多下游任务

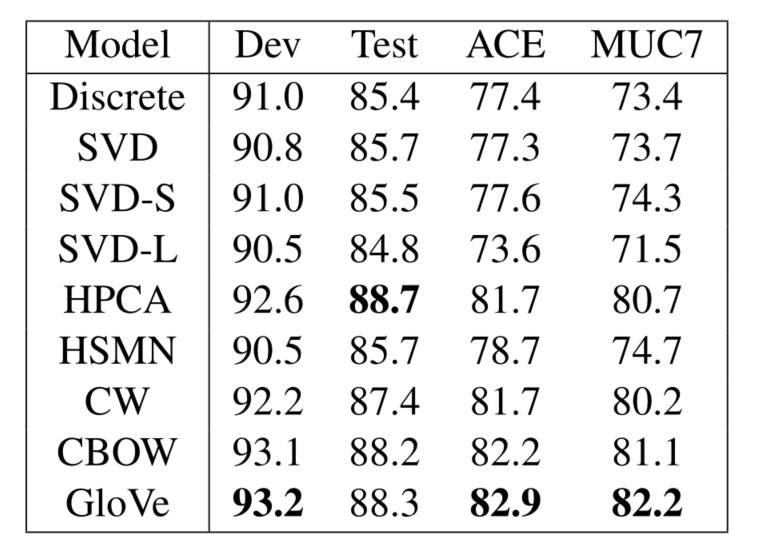
20221001220254-2022-10-01-22-02-55

一个例子是在命名实体识别任务中，寻找人名、机构名、地理位置名，词向量非常有帮助